aplikasi perbandingan trigonometri

Aplikasi Perbandingan Trigonometri Contoh Soal : Andre mengukur tinggi pohon yang ada di belakang rumahnya. Tinggi pohon tersebut akan sulit diukur menggunakan meteran. Oleh karena itu Andre akan menggunakan perbandingan trigonometri untuk mengukur tinggi pohon tersebut. Andre berdiri dengan jarak 5 meter dari pohon dan menatap pucuk pohon dengan sudut elevasi 60

Oleh Diposting pada

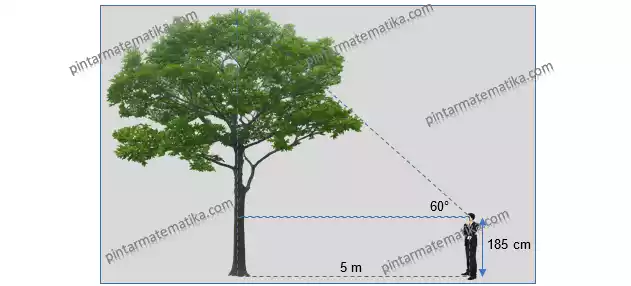
Aplikasi Perbandingan Trigonometri

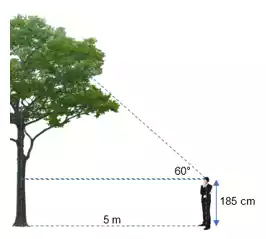aplikasi perbandingan trigonometriAndre mengukur tinggi pohon yang ada di belakang rumahnya. Tinggi pohon tersebut akan sulit diukur menggunakan meteran. Oleh karena itu Andre akan menggunakan perbandingan trigonometri untuk mengukur tinggi pohon tersebut. Andre berdiri dengan jarak 5 meter dari pohon dan menatap pucuk pohon dengan sudut elevasi 60° (lihat contoh sketsa). Jika tinggi  Andre dari tanah 185 cm maka tinggi pohon tersebut adalah…. (√3= 1,73)

  1. 10,35 m
  2. 10,40 m
  3. 10,45 m
  4. 10,50 m
  5. 10,55 m

Contoh soal tersebut merupakan bentuk soal penalaran dari materi perbandingan trigonometri kelas 10, mari kita kupas tuntas materinya kemudian kita selesaikan pembahasannya.

 

Perbandingan Trigonometri

Pada segitiga siku siku, sisi sisi yang bersesuaian dapat diberi istilah untuk memudahkan materi perbandingan trigonometri. Perhatikan gambar berikut dan penjelasannya!

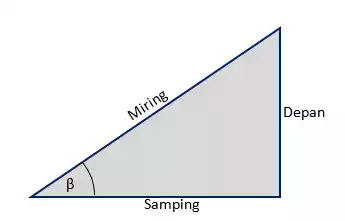
Penjelasan :

  1. Sisi depan adalah sisi yang berada di depan sudut β
  2. Sisi samping adalah sisi yang berada di samping sudut β
  3. Sisi miring adalah sisi yang berada di depan sudut siku siku.

Hubungan perbandingan sudut lancip dengan panjang sisi sisi suatu segitiga siku siku dinyatakan dengan definisi berikut

Aplikasi perbandingan trigonometri

Dalam soal penalaran matematika UTBK aplikasi perbandingan trigonometri sering digunakan terutama untuk mengukur jarak dua objek dan ketinggian benda.

A.   Jarak Dua Objek

Misalkan diketahui dua buah objek missal A dan B diamati dari satu titik yang sama dengan sudut tertentu, dapat dihitung jarak keduanya, perhatikan ilustrasi.

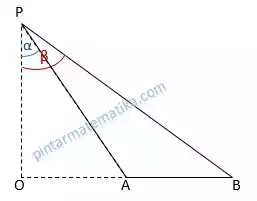
Baca Juga  pembahasan soal limit fungsi trigonometri 1

Keterangan:
P : titik pengamatan
O : titik imajiner (OP tegak lurus OB)
A : titik objek A
B : titik objek B
Jarak objek A dan B adalah jarak O ke B dikurangi jarak O ke A
Dengan perbandingan trigonometri (sisi depan disbanding sisi samping atau tangen) diperoleh

Sehingga

Jadi dapat disimpulkan untuk ilustrasi seperti di atas, rumus jarak dua objek adalah
AB = OP(tanβ – tanα)

B.    Menghitung Ketinggian Objek

Serupa dengan menghitung jarak dua objek, ketinggian suatu benda atau objek yang diamati dari suatu titik tertentu dengan sudut elevasi tertentu juga dapat dihitung dengan perbandingan trigonometri.

Misal seorang pengamat pada titik P dengan ketinggian mata Tm mengamati objek A dengan sudut elevasi α, ketinggian objek dapat dihitung seperti ilustrasi berikut.

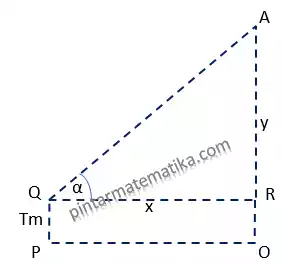
Keterangan:

PQ = ketinggian mata pengamat (Tm)
PO = jarak pengamat ke objek teramati (x)
AR = ketinggian objek dari mata pengamat (y)
α = sudut elevasi (sudut pengamatan)

Ketinggian (h) objek A selanjutnya disebut OA
OA = OR + RA
h = Tm + y
y diperoleh dengan perbandingan trigonometri sisi depan dengan sisi samping atau tangen alpha


maka
y = x.tanα
sehingga
h = Tm + y
h = Tm + x tanα

Contoh soal dan Pembahasan

Nomor 1

Diketahui suatu segitiga siku siku dengan tangen salah satu sudut lancipnya . Nilai sinus dan kosinusnya berturut-turut adalah….

Pembahasan

Dari soal diketahui karena
maka diketahui panjang sisi depan 8 dan panjang sisi samping 15

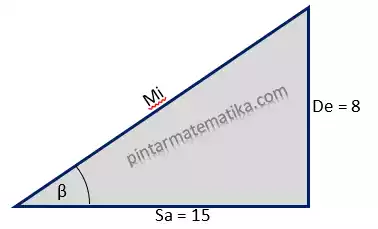
Sisi miring dapat dihitung dengan teorema pythagoras, atau diambil dari triple Pythagoras 8, 15 dan 17 maka dapat disimpulkan panjang sisi miring 17. Dengan demikian berlaku

Jawaban A

 

Nomor 2

Diketahui segitiga PQR siku siku di Q, jika PQ = 28 cm dan QR = 45 cm dengan β merupakan sudut QPR,  hitunglah nilai sin β !

Pembahasan

Pertama mari kita sajikan keterangan soal dalam bentuk ilustrasi gambar seperti pada nomor 1

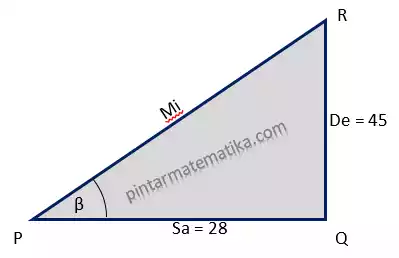
Baca Juga  Dewi melakukan pelemparan dua buah dadu satu kali. Variabel acak 𝑋 menyatakan jumlah kedua mata dadu

Dengan menggunakan teorema pythagoras dapat diperoleh panjang sisi miring

Sehingga diperoleh

 

Contoh Soal Penalaran ( Aplikasi ) dan Pembahasannya

Andre mengukur tinggi pohon yang ada di belakang rumahnya

1.   Andre mengukur tinggi pohon yang ada di belakang rumahnya.Tinggi pohon tersebut akan sulit diukur menggu

nakan meteran. Oleh karena itu, Andre akan menggunakan perbandingan trigonometri untuk mengukur tinggi pohon tersebut. Andre berdiri dengan jarak 5 meter dari pohon dan menatap pucuk pohon dengan sudut elevasi 60° (lihat contoh sketsa). Jika tinggi Andre dari tanah 185 cm maka tinggi pohon tersebut adalah…. (√3= 1,73)

        1. 10,35 m
    2. 10,40 m
    3. 10,45 m
    4. 10,50 m
    5. 10,55 m

 

Pembahasan

Tinggi pohon (Tp) berarti tinggi pandangan Andre (Tm)  ditambah tinggi pohon diatas pandangan Andre (y)


Diketahui tinggi pandangan Tm = 185 cm atau 1,85 m
Langkah berikutnya kita hitung y

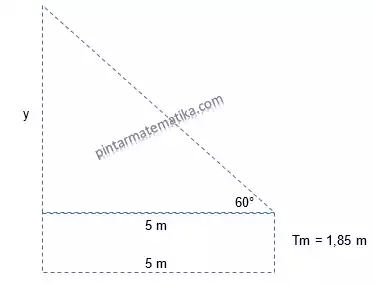
y dapat dihitung dengan perbandingan sisi depan (sudut 60°) dengan sisi samping (sudut 60°) atau disebut dengan tangen sebagai berikut

Dengan demikian

Jawaban D

Seorang anak berdiri dengan jarak 12 m

2 .   Seorang anak berdiri dengan jarak 12 m dari sebuah pohon, dia mengamati 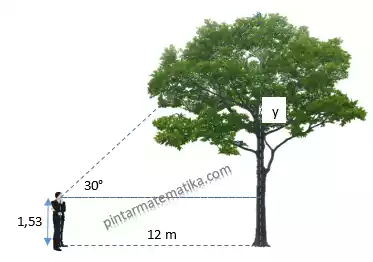pucuk pohon dengan sudut elevasi 30°. Jika tinggi pandangan (mata) anak tersebut dari tanah adalah 153 cm dan nilai dari √3= 1,73, maka tinggi pohon tersebut adalah….(perhatikan ilustrasi gambar!)

  1. 8,15 m
  2. 8,27 m
  3. 8,38 m
  4. 8,45 m
  5. 8,52 m

Pembahasan

Dengan menggunakan cara praktis dapat dihitung tinggi pohon sebagai berikut

Diket x = 12 m

Tm = 1,53 m

 α = 30°

maka ketinggian (h)

h = Tm + x tanα

h = 1,53 + 12 tan30°

h = 1,53 + 12 . ⅓√3

h = 1,53 + 4 . 1,73

h = 1,53 + 6,92

h = 8,45 m

Jawaban D

Contoh soal serupa Disini

 

 

*******

Lebih banyak pembahasan soal-soal Persiapan UTBK (Penalaran Matematika) dapat anda baca di

Baca Juga  Pak Andi akan memagari kebunnya menggunakan waring

kunjungi kak RH YT Channel : taklukan soal UTBK 

 

Posting terkait: