Sebuah denah peternakan
Sebuah denah peternakan diketahui memiliki ukuran 14 cm x 8 cm seperti gambar berikut.
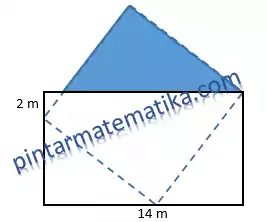
Area berwarna biru adalah kolam ikan yang jika ditarik garis merupakan bagian dari area berbentuk persegi. Luas kolam adalah….
- 31 m²
- 33,75 m²
- 35,25 m²
- 36 m²
- 37,5 m²
Pembahasan
Sobat pintar matematika, sebelum menyelesaikan pembahasan soal tersebut ijinkan saya kupas sedikit materi dasar yang menjadi modal penyelesaian , tentulah sobat pintar matematika pernah mempelajarinya pada jenjang SMP dan SMA. pengulasan singkat materidasar berikut seyogyanya menjadi pengingat atau review untuk membangkitkan ingatan kita pada materi yang mungkin sudah lama tidak dipelajari.
Soal tersebut merupakan materi geometri bangun datar. Beberapa teknik yang harus dikuasai yaitu sub materi luas bangun datar (segitiga siku-siku) , teorema Pythagoras dan kesebangunan pada segitiga.
LUAS SEGITIGA
Perhatihan gambar berikut
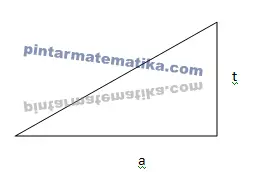
Secara umum luas segitiga siku-siku dengan alas a dan tinggi t seperti pada gambar tersebut dapat dihitung dengan rumus L=½.a.t
TEOREMA PYTHAGORAS
berdasarkan gambar diatas, jika dimisalkan sisi miring adalah c maka terdapat tiga hubungan antar sisi menurut teorema pythagoras yaitu sebagai berikut:
c² = a² + t²
a² = c² – t²
t² = c² – a²
KESEBANGUNAN SEGITIGA
Materi pendukung yang digunakan pada soal ini juga mencakup materi kesebangunan pada segitiga, materi ini merupakan materi dasar yang dipelajari di SMP kelas 8 (Sekolah Menengah Pertama kelas delapan).
untuk memahaminya perhatikan gambar berikut
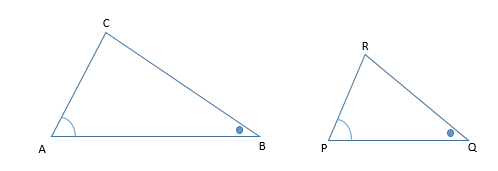
segitiga ABC dan segitiga PQR memiliki ciri khusus yang identik dimana sudut A sama dengan sudut P, sudut B sama dengan sudut Q sedemikian sehingga mengakibatkan sudut C sama dengan sudut R
keadaan yang demikian memenuhi syarat bahwa segitiga ABC sebangun dengan segitiga PQR sehingga berlaku sisi-sisi yang bersesuaian sebanding
sisi AB sebanding dengan sisi PQ
sisi BC sebanding dengan sisi QR
sisi AC sebanding dengan sisi PR
SELANJUTNYA MARI KITA SELESAIKAN SOAL TERSEBUT
Perhatikan gambar denah dengan sedikit garis bantu, area kolam akan sama dengan area diarsir pada persegi panjang, sehingga beberapa keterangan ukuran dapat disesuaikan sesuai gambar berikut
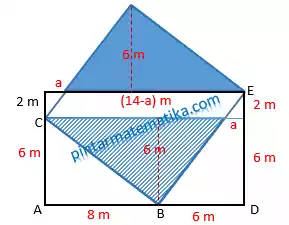
Persegi panjang terpotong persegi dimana tiga titik sudut tepat menyentuh sisi persegi mengakibatkan area segitiga ABC dan segitiga BDE kongruen sehingga dapat dituliskan rincian ukuran kedua segitiga tersebut seperti pada gambar tersebut.
Berikutnya akan dihitung luas kolam (misal K)
K merupakan segitiga dengan alas (14-a) m dengan tinggi 6 meter, dengan menggunakan rumus luas segitiga kita hitung luas kolam (misal K) sebagai berikut
dalam perhitungan diperoleh persamaan luas kolam dalam a, dengan demikian kita memerlukan nilai a.
untuk memperoleh nilai a mari memanfaatkan perbandingan pada segitiga-segitiga yang sebangun, dalam kasus ini kita menggunakan segitiga BDE yang terpotong garis sepanjang a.
Perhatikan segitiga BDE
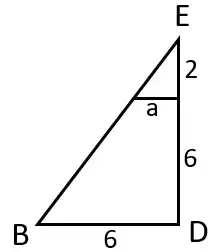
dari gambar diperlihatkan sudut DBC sama dengan sudut kecil yang dibentuk garis a dengan sisi BE kemudian sudut BDE bernilai 90 derajat senilai dengan sudut yang dibentuk garis a dengan sisi DE, sementara sudut BCD pada puncak segitiga senilai dengan sudut C pada segitiga kecil, dari keterangan tersebut dapat disimpulkan segitiga-segitiga tersebut sebangun.
dikarenakan kedua segitiga tersebut sebangun maka memenuhi perbandingan sisi-sisi yang bersesuaian
sisi BD sebanding dengan sisi a pada segitiga kecil
sisi DC sebanding dengan sisi berukuran 3 meter pada segitiga kecil
perbandingan yang demikian dapat dimanfatkan untuk melakukan perhitungan sebagai berikut
nilai a yang sudah ditemukan kemudian disubtitusikan kedalam persamaan luas kolam (K)
Dengan demikian luas Kolam K adalah
Jawaban E
Demikian penjelasan terperinci dari soal tersebut, sebagai catatan dua bangun atau lebih dikatakan sebangun apabila memenuhi dua syarat yaitu
- sudut-sudut yang bersesuaian sama besar
- sisi-sisi yang bersesuaian sebanding
dalam kasus segitiga segitiga yang sebangun, terdapat keistimewaan yang akan mempermudah kita dalam mengingatnya. Dua segitiga dikatakan sebangun apabila memenuhi keadaan sebagi berikut:
a. Sudut, Sisi, Sudut
dua buah segitiga dengan dua sudut yang seletak sama besar dipastikan sebangun
b. sisi, sudut, sisi
dua buah segitiga dengan dua sisi sebanding dengan dua sisi segitiga yang lain dan sudut-sudut yang mengapit sama besar, maka segitiga-segitiga tersebut sebangun.
c. sudut, sudut, sudut
dua buah segitiga dengan ketiga sudutnya sama besar, maka segitga-segitiga tersebut sebangun
*******
Lebih banyak pembahasan soal-soal Persiapan UTBK (Penalaran Matematika) dapat anda baca di
kunjungi kak RH YT Channel : taklukan soal UTBK


