Nilai Diskriminan Persamaan Kuadrat
Menentukan nilai diskriminan Persamaan kuadrat dengan
dan
dapat menggunakan formula berikut
.
Dilihiat dari nilai diskriminan, persamaan kuadrat dapat dibedakan menjadi tiga tipe berbeda, yaitu:
, Persamaan kuadrat tidak memiliki akar riil
, Persamaan kuadrat memiliki dua akar riil yang sama
, Persamaan kuadrat memiliki dua akar riil yang berbeda
contoh soal dan pembahasan menentukan akar akar persamaan kuadrat dapat diakses DI SINI
Contoh Soal dan Pembahasan
Nomor 1
Persamaan kuadrat px²-4x+3=0 mempunyai akar-akar real yang sama. Nilai p yang memenuhi adalah….
Pembahasan

Jawaban A
Nomor 2
Nilai diskriminan persamaan kuadrat adalah 1, tentukan nilai p !
Penyelesaian
![]()
diketahui a=1, b=7, c=p dan D=1
Nomor 3
Nilai m yang memenuhi agar persamaan kuadrat tidak memiliki akar riil adalah…
Pembahasan
perhatikan dari persamaan kuadrat diketahui a = 2, b = (m+7) dan
.
syarat suatu persamaan kuadrat tidak memiliki akar akar riil, diskriminan harus bernilai kurang dari nol (D<0).
pembuat nol sebagai berikut
Kemudian buatlah garis bilangan untuk membantu menentukan daerah penyelesaian

Pilih bilangan bukan -6 atau 8 kemudian subtitusikan ke untuk menentukan tanda positif atau negative pada area garis bilangan. Pada contoh ini saya memilih nol (0) sebagai penguji.
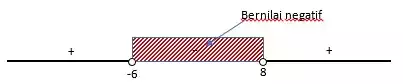
Karena syarat D<0 maka daerah penyelesaian kita pilih yang negative, sehingga nilai m yang memenuhi supaya persamaan kuadrat tidak memiliki akar akar riil adalah
Jawaban A
Nomor 4
Persamaan kuadrat mempunyai akar-akar kembar, nilai m yang memenuhi adalah….
- -2
- -3
- -4
- -5
- -6
Penyelesaian
akar kembar atau akar sama berarti diskriminan persamaan kuadrat tersebut sama dengan nol
jawaban A
Demikian materi dan contoh soal bagus yang kak RH sajikan akan menjadi referensi belajar dan persiapan UTBK nantinya.
semoga sukses
Banyak pembahasan soal-soal Matematika Kelas X dapat anda baca pada postingan sebelumnya
kunjungi kak RH YT Channel : taklukan soal UTBK untuk belajar hal hal menarik lainnya
Semoga bermanfaat.




