Barisan geometri
Barisan geometri merupakan barisan yang suku sukunya diperoleh dengan mengalikan suku suku sebelumnya dengan bilangan yang tetap, bilangan ini kemudian disebut dengan rasio disimbolkan r.
Suku pertama barisan goemetri disimbolkan dengan huruf a (U1=a) sehingga suku kedua (U2) hasil dari suku pertama kali rasio dituliskan sebagai U2=a.r
mari pahami susunan suku suku berikut:
U1 = a
U2 = ar
U3 = ar.r = ar2
U4 = ar2.r = ar3
U5 = ar3.r = ar4
U6 = ar4.r = ar5
Dapat diperhatikan terdapat pola yang tetap dimana untuk suku ke n (Un) diperoleh rumus suku ar(n-1) dengan memperhatikan pola tersebut, untuk mencari suku ke-n barisan geometri dapat digunakan rumus
Un=ar(n-1)
Deret Geometri
Setiap suku suku barisan geometri yang dijumlahkan dapat disebut sebagai deret geometri, selanjutnya deret geometri disimbolkan dengan Sn diistilahkan dengan jumlan n suku pertama barisan geometri.
ada dua rumus untuk ini, bergantung pada rasionya
a) menentukan jumlah n suku pertama barisan geometri dengan r < 1
b) menentukan jumlah n suku pertama barisan geometri dengan r > 1
Deret Geometri Tak Hingga
Deret geometri tak hingga memiliki suku suku tak hingga banyaknya, deret geometri yang memiliki batasan jumlah hanya deret geometri dengan rasio antara nol dan satu (0 < r < 1).
rumus untuk menentukan jumlah suku suku pada deret geometri tak hingga sebagai berikut
Contoh Soal dan Pembahasan
Nomor 1
Diketahui barisan geometri dengan suku kedua adalah 15 dan suku keempat adalah 135. Jika rasio barisan tersebut positif, suku kedelapan barisan geometri tersebut adalah….
A 10933
B 10934
C 10935
D 10936
E 10937
Pembahasan
U2 = 15 ⇒ ar = 15
U4 = 135 ⇒ ar3 = 135
langkah berikutnya mencari rasio dan suku pertama dengan membandingkan dua suku yang sudah diketahui sebagai berikut
Dipilih r = 3 (positif)
akan dicari suku ke 8 atau U8
Jawaban C
Nomor 2
Pertambahan penduduk di suatu desa setiap tahunnya membentuk barisan geometri. Pada tahun 2021, penduduk bertambah sebanyak 10 orang, lalu pada tahun 2023 sebanyak 90 orang. Jumlah pertambahan penduduk pada tahun 2025 adalah….
- 270
- 343
- 420
- 720
- 810
Pembahasan
Diketahui
Maka berlaku
karena dalam soal disebut pertambahan penduduk maka r = -3 tidak berlaku sehingga rasio yang memenuhi adalah r = 3
Jumlah pertambahan penduduk pada tahun 2025 (suku ke-5)
Jawaban E
Nomor 3
Seorang anak melompat di atas trampoline. Dalam sekali ayun, pantulan pertama setinggi 120 cm. tinggi pantulan berikutnya hanya ¼ tinggi sebelumnya. Panjang lintasan seluruhnya sampai bola berhenti adalah….
- 120 cm
- 230 cm
- 320 cm
- 420 cm
- 437 cm
Pembahasan
Perhatikan ilustrasi masing masing lompatan berikut
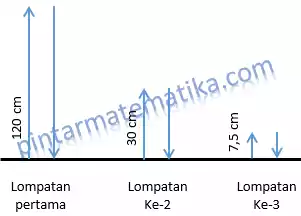
Panjang lintasan artinya panjang seluruh lintasan naik dan seluruh lintasan turun
Jawaban C
Nomor 4
Sebuah bola menggelinding diperlambat dengan kecepatan tertentu. Pada detik pertama jarak yang ditempuh 10 meter, detik ke-2 8 meter, detik ketiga 6,4 meter danseterusnya mengikuti pola barisan geometri. Jarak yang ditempuh bola sampai berhenti adalah….
- 38 m
- 46 m
- 50 m
- 57 m
- 59 m
Diketahui
Pembahasan
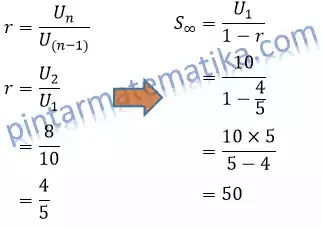
Jawaban C
Nomor 5
Persegi ABCD mempunyai panjang 24 cm. Persegi baru terbentuk dengan menghubungkan setiap titik tengah dari sisi persegi ABCD. Jika proses tersebut diulang tak berhingga, tentukan jumlah keliling persegi-persegi tersebut!
Pembahasan
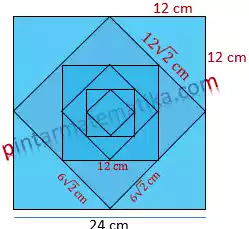
Keliling-keliling tersebut membentuk deret sebagai berikut
Demikian paparan materi Barisan dan deret goemetri beserta contoh aplikasi soal dan pembahasanya, akan sangat bermanfaat sebagai referensi belajar persiapan ASAS, Ujian Sekolah dan Persiapan Seleksi Masuk Perguruan Tinggi atau UTBK SNBT
Materi, contoh soal dan pembahasan barisan aritmatika dapat dibaca DISINI
Lebih banyak pembahasan soal-soal dapat anda baca di Persiapan UTBK (Penalaran Matematika)
kunjungi kak RH YT Channel : taklukan soal UTBK



