Teorema Sisa
Suatu polinomial P(x) dibagi oleh pembagi f(x) memiliki hasil H(x) dan sisa pembagian S(x). sering dituliskan dalam persamaan dasar sebagai:
Pada pembagian p0linomial atau suku banyak, umumnya terdapat tiga tipe pembagi terdiri dari pembagi linier dan berderajat n. Tiga tipe pembagi ini memunculkan teorema sisa sebagai berikut:
Teorema Sisa 1 : Pembagi berbentuk (x – k)
Suku banyak P(x) berderajat n dibagi (x – k) memiliki sisa pembagian P(k)
Contoh
Tentukan sisa pembagian suku banyak P(x) = x² – 4x + 5 oleh (x + 2) !
Pembahasan
suku banyak P(x) = x² – 4x + 5 dibagi dengan x + 2, sisanya S(x) = P(-2)
nilai P(-2) dapat dihitung sebagai berikut
P(x) = x² – 4x + 5
P(-2) = (-2)² – 4(-2) + 5 = 4 + 8 + 5 = 17
P(-2) = 17
∴ sisa pembagian S(x) = P(-2) = 17
Teorema Sisa 2 : Pembagi berbentuk (ax – b)
Suku banyak P(x) berderajat n dibagi (ax – b) memiliki sisa pembagian P(b/a)
Contoh
tentukan sisa pembagian polinomial f(x)=2x³+9x²-2x+5 oleh (2x+1) !
Pembahasan
Cara I
dibagi oleh (2x+1)
maka sisanya f(-1/2)
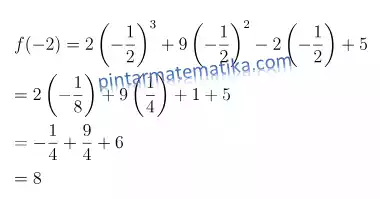
Teorema Sisa 3 : Pembagi berbentuk (x – m)(x – n)
Suku banyak P(x) berderajat n dibagi (x – a) (x – b) memiliki sisa pembagian
Contoh
Suku banyak f(x) jika dibagi (x – 2) sisanya 24 dan dibagi (x + 5) sisanya 10. apabila

Pembahasan
Cara 1 (dengan rumus)
diketahui
x – a = x – 2 maka a = 2 dan f(2) = 24
x – b = x + 5 maka b = -5 dan f(-5) = 10
dengan rumus sisa, dapat dihitung sebagai berikut
Cara 2 (dengan memisalkan S(x) = ax+b)
F(x) jika dibagi sisanya 24 maka
F(x) jika dibagi sisanya 10 maka
Jika diketahui formula sisa pembagian
dari dua persamaan tersebut kita lakukan eliminasi dan subtitusi sebagai berikut

jadi sisa pembagian
jawaban D
Bonus Contoh Soal dan Pembahasan
Nomor 1
Polinomial f(x) = 2x³- px² + qx + 6 dan g(x) = 2x³ + 3x² – 4x – 5 mempunyai sisa yang sama jika dibagi oleh (x + 1). Tentukan (p + q) !
Pembahasan
sisa pembagian f(x) oleh (x+1) adalah f(-1)
sisa pembagian g(x) oleh (x+1) adalah g(-1)
karena keduanya bernilai sama, maka berlaku

Nomor 2
Suku banyak f(x) jika dibagi oleh (x + 4) bersisa 12 dan f(x) habis dibagi x2 – 4. Sisa pembagian f(x) jika dibagi adalah…
- -2x – 4
- -2x + 4
- 2x – 4
- x + 2
- x – 2
Pembahasan
f(x) dibagi (x + 4) bersisa 12 maka f(-4) = 12
f(x) habis dibagi (x2 – 4) maka f(-2) = 0 atau f(2) = 0
Jika diketahui formula sisa pembagian
dari dua persamaan tersebut kita lakukan eliminasi dan subtitusi sebagai berikut

jadi Sisa pembagian f(x) jika dibagi adalah ax + b = -2x + 4
Jawaban B
Nomor 3
Suku banyak dibagi oleh
, hasil bagi dan sisanya berturut-turut adalah ….
A x² – 3x – 10 dan 0
B x² – 5x – 12 dan 0
C x² – 5x – 12 dan 5
D x² – 11x – 20 dan 5
E x² – 9x – 30 dan 0
Pembahasan

Jawaban A
Nomor 4
Suku banyak f(x) dibagi dengan (x + 2) mempunyai sisa 14, dibagi dengan (x – 4) mempunyai sisa -4. Sisa pembagian f(x) jika dibagi dengan (x² – 2x – 8) adalah….
Pembahasan
pembagi
f(x) dibagi dengan (x + 2) bersisa f(-2)=14 sedangkan
f(x) dibagi dengan (x – 4) bersisa f(4) = -4

Jadi sisa pembagian f(x) oleh (x² – 2x – 8) adalah
Demikian paparan materi teorema sisa suku banyak beserta contoh soal dan pembahasannya dapat dijadikan referensi belajar persiapan ASAT, Ujian Sekolah maupun persiapan Seleksi Masuk Perguruan Tinggi UTBK.
Lebih banyak pembahasan soal-soal Matematika Kelas XI dapat anda baca pada pintarmatematika.com
kunjungi kak RH YT Channel : taklukan soal UTBK untuk belajar hal hal menarik lainnya
Semoga bermanfaat.




