Tabung merupakan bagian materi dari bab Bangun Ruang Sisi Lengkung yang dibahas di kelas Sembilan Sekolah Menengah Pertama. Selain tabung, bab ini membahas Kerucut dan bola.
Pada tulisan kak RH kali ini, akan sahabat pintar matematika pelajari mengenai tabung yaitu tentang jaring-jaring dan bagian-bagiannya kemudian dibahas luas serta volume tabung disertai dengan contoh soal dan pembahasan detainya.
Tabung
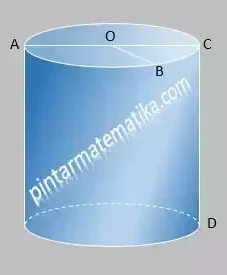Gambar di samping merupakan sebuah tabung.
Tabung terdiri atas sisi alas yang selanjutnya disebut dengan alas tabung, sisi lengkung yang dikenal dengan istilah selimut tabung dan terahir adalah sisi atas selanjutnya disebut sebagai tutup tabung.
Berdasar gambar di samping, dijelaskan bagian bagian sebagai berikut:
-
-
-
-
-
-
- garis AC disebut diameter atau garis tengah tutup dan alas tabung
- garis CD disebut tinggi tabung
- garis OA, OB dan OC disebut jari jari tabung, selanjutnya diketahui bahwa nilai/panjang jari-jari alas dan atap tabung merupakan setengah nilai diameternya.
-
-
-
-
-
Ciri-ciri Tabung :
- Tabung memiliki tiga sisi yaitu dua sisi datar yang berbentuk lingkaran dengan jari-jari yang sama dan kongruen. Serta memiliki satu sisi lengkung.
- Tabung tidak memiliki titik sudut.
- Tabung memiliki dua rusuk. Yaitu rusuk pada alas dan rusuk pada sisi atas
- Jarak antara sisi alas dan sisi atas tabung disebut tinggi tabung
Jaring-jaring tabung
Perhatikan gambar tabung berikut:
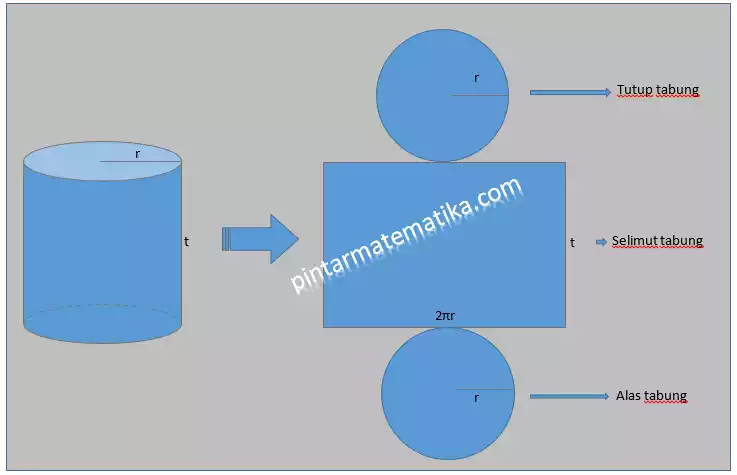
Tabung (seperti gambar kiri) apabila dipotong sesuai bagian-bagiannya berbentuk bangun datar atau selanjutnya disebut jarring-jaring tabung (seperti gambar bagian kanan) terdiri atas:
- Alas tabung, alas tabung berbentuk lingkaran dengan jari jari r atau diameter d = 2r
- Selimut tabung, selimut tabung berbentuk persegi panjang dengan panjang sama dengan keliling alas tabung atau keliling lingkaran dengan jari jari r, sehingga panjang selimut tabung dituliskan p = 2πr dengan lebar sama dengan tinggi tabung atau l = t
- Tutup tabung, tutup tabung selalu sama dan sebangun dengan alas tabung. Berbentuk lingkaran dengan jari jari r sama besar dengan r pada alas tabung.
Luas Tabung
Dari jaring jaring tabung / bagian bagian tabung kita bias rumuskan luas permukaan tabung dengan menghitung luas masing masing bagian, sebagai berikut:
- Alas Tabung
Luas alas tabung = πr²
- Selimut Tabung
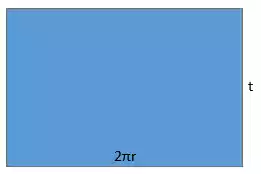
Luas selimut tabung = Luas persegi panjang = p x l
Luas selimut tabung = 2πrt
- Tutup tabung
Karena tutup tabung sama dan sebangun dengan alas tabung, maka luas tutup tabung sama dengan luas alas tabung
Luas tutup tabung = πr²
Dengan menambahkan semua luas bagian bagan tabung akan diperoleh luas permukaan tabung sebagai berikut:
Luas permukaan tabung (Lt) = Luas alas (La) + Luas selimut (Ls) + Luas tutup (La)
Lt = La + Ls + La
Lt = 2La + Ls
Lt = 2 πr² + 2πrt
Lt = 2πr (r + t)
Jadi Luas permukaan tabung
Lt = 2πr (r + t)
Volume Tabung
Seperti telah disebutkan di awal, tabung memiliki sisi alas yang sama dan sebangun (kongruen) dengan sisi atas atau sisi tutupnya. Dari informasi tersebut dapat disimpulkan bahwa tabung merupakan salah satu prisma dengan alas berbentuk lingkaran.
Untuk menentukan volume tabung, kita dapat gunakan rumus volume prisma
Volume prisma = Luas alas × tinggi
karena alas tabung berbentuk lingkaran, dan luas lingkaran = πr² maka volume tabung dapat dituliskan
Volume tabung = πr² × t
V = πr²t
Keterangan:
V = Volume tabung
π = phi = 3,14 atau 22/7
r = jari-jari alas atau tutup tabung
t = tinggi tabung
Nah sobat pintar matematika, untuk lebih memahami tentang luas dan volume tabung perhatikan contoh soal dan pembahasan berikut.
Contoh Soal dan Pembahasan
1. Sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm, hitunglah:
- Volume tabung
- luas tabung
Pembahasan
Diketahui :
r = 7 cm
t = 10 cm
π = 22/7
Jawaban
a. Volume tabung
V = πr² × t
V= 22/7 . 7². 10
V = 1540 cm³
b. Luas Tabung
L = 2πr (r + t)
L = 2. 22/7 . 7 (7 + 10)
L = 748 cm²
2. Sebuah wadah berbentuk tabung dengan diameter alas 14 cm penuh berisi air. ke dalam wadah dimasukan sebuah kubus logam dengan rusuk 10 cm, volume air yang tumpah adalah….
Pembahasan
dari soal tersebut diketahui
tabung : d = 14 cm maka r = (1/2)d = (1/2)14 = 7 cm
kubus : s = 10 cm
Demikian pembahasan materi Tabung : Jaring-jaring, Luas, Volume Contoh Soal dan Pembahasannya, sampai jumpa ditulisan tulisan pintar matematika berikutnya semoga bermanfaat.
∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗
Untuk pengalaman belajar dan referensi belajar lebih banyak ada di
Pembahasan Soal Soal Matematika kelas 9
kunjungi kak RH YT Channel untuk menonton video pembahasan soal-soal matematika
