Pola bilangan,
Dalam kehidupan sehari-hari sering kita temui banyak hal yang erat kaitannya dengan pola bilangan. Salah satu yang sedang sering dialami masyarakat adalah adanya rute ganjil genap pada kendaraan bermotor. Tahukah kalian bahwa plat ganjil genap ini sebenarnya membentuk pola bilangan yaitu pola bilangan ganjil dan pola bilangan genap.
Pada kasus keseharian yang lain, pemandu sorak misalnya memiliki formasi piramida (yang sebetulnya berbentuk segitiga ke atas) Jika piramida 2 tingkat maka dibutuhkan 3 orang dengan dua orang di bawah dan satu di puncak piramid, sementara jika piramida 3 tingkat maka dibutuhkan enam orang dengan formasi 3 orang di bawah dua di tingkat berikutnya dan satu di puncak, jika piramida 4 tingkat akan dibutuhkan 10 orang dan jika piramida 5 tingkat maka jumlah orang yang dibutuhkan 15 orang dan seterusnya membentuk pola yang tetap.
Masih banyak kejadian sehari-hari yang erat kaitannya dengan pola bilangan, seperti pola yang terbentuk pada pembelahan mitosis sel, susunan bola pada awal permainan bola sodok, perkembangbiakan amoeba dan lain lain.
Definisi Pola Bilangan
Pola memiliki arti bentuk atau struktur yang tetap, dan arti kata bilangan menurut KBBI merupakan satuan dalam sistem matematis yang abstrak dan dapat diunitkan, ditambah, atau dikalikan.
Pola bilangan dapat didefinisikan sebagai bentuk atau susunan yang tetap pada bilangan-bilangan dengan aturan tertentu.
Dalam pola bilangan tedapat suku-suku dengan aturan dan symbol tertentu, sebagai contoh 2, 4, 6, 8, 10,…
2 disebut sebagai suku pertama, 4 suku ke-2, 6 suku ke-3 dan seterusnya, Suku pertama biasanya dimisalkan dengan a sedangkan suku ke-n disimbolkan dengan Un sebagai contoh pada pola bilangan tersebut suku ke-5 dapat ditulis U₅ = 10.
Jenis Jenis Pola Bilangan
Pola Bilangan Ganjil
Pola bilangan genap merupakan pola bilangan yang tersusun dari bilangan bilangan ganjil berurutan dari yang terkecil yaitu 1, 3, 5, 7, 9, …
Pola bilangan ganjil digambarkan sebagai berikut:

Suku-suku pada pola bilangan ganjil dapat diperoleh dengan rumus
Un = 2n – 1
Pola Bilangan Genap
Seperti halnya pola bilangan ganjil, pola bilangan genap merupakan pola bilangan yang tersusun dari bilangan bilangan genap berurutan dari yang terkecil yaitu 2, 4, 6, 8, …
Dalam bentuk gambar dapat diilustrasikan sebagai

Suku-suku pada pola bilangan genap dapat dihitung dengan rumus
Un = 2n
Pola Bilangan Segitiga
Pola / susunan bilangan-bilangan yang jika disajikan secara geometri bentuknya merupakan bangun datar segitiga
Contoh pola bilangan segitiga yaitu 1, 3, 6, 10, …
Secara goemetri dapat disajikan sebagai berikut
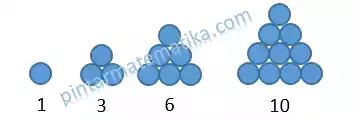
Suku-suku pada pola bilangan segitiga dapat dihitung dengan rumus
Un = ½n (n + 1)
Pola Bilangan Persegi
Pola / susunan bilangan-bilangan yang jika disajikan secara geometri bentuknya merupakan bangun datar bujur sangkar
Contoh pola bilangan segitiga yaitu 1, 4, 9, 16, 25, …
Secara goemetri digambarkan

Suku-suku pada pola bilangan persegi dapat dihitung dengan rumus
Un = n²
Pola Bilangan Persegi Panjang
Pola / susunan bilangan-bilangan yang jika disajikan secara geometri bentuknya merupakan bangun datar persegi panjang
Contoh 2, 6, 12, 20, …
Secara geometri digambarkan
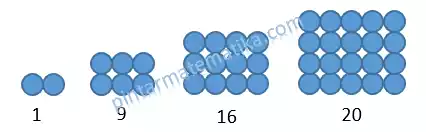
Suku-suku pada pola bilangan persegi panjang dapat dihitung dengan rumus
Un = n (n + 1)
Pola Bilangan Pada Segitiga Pascal
Blaise Pascal seorang filsuf dan ilmuwan yang berasal dari Perancis yang menemukan pola segitiga ini, segingga disebut segitiga pascal. Nama Blaise Pascal tentu saja tidak asing ditelinga kita, dalam ilmu fisika Pascal sangat berjasa dengan hokum-hukum Pascalnya.
Pascal menjumlahkan setiap dua bilangan pada barisan pertama dan menuliskan hasilnya tepat diantara dua barisan tersebut pada baris berikutnya, dan seterusnya diulang dengan cara yang sama kemudian menuliskan angka satu (1) pada setiap awal dan ahir baris bilangan yang terbentuk. Untuk memahaminya perhatikan ilustrasi segitiga pascal berikut.

Dari gambar tersebut terlihat bahwa jumlah masing-masing baris dihubungkan dengan baris berikutnya membentuk suatu pola yang tetap 1, 2, 4, 8, 16, 32 …
Suku-suku yang terbentuk dapat diperoleh dengan menggunakan formula
Pola Bilangan Fibonacci
Bilangan bilangan pada pola Fibonacci diperoleh dengan menjumlahkan dua angka sebelumnya secara berurutan. Contoh : 1, 1, 2, 3, 5, 8, 13, …
Suku suku pola bilangan Fibonacci dapat dirumuskan sebagai
Soal dan Kunci Jawaban
1 . 14, 15, 17, 18, 20, 21, 23, 24, dan ….
- 25
- 26
- 27
- 28
- 29
Jawaban D
2. 1, -2, -6, 12, 36, …, ….
- -48, -124
- 48, 144
- 72, 216
- -72, -216
- -58, 124
Jawaban D
3. 60, 10, 70, 7, 80, 4, 90, dan X. Berapakah X?
- 1
- 100
- 2
- 110
- 104
Jawaban A
Soal Lengkap Di sini
*******
Lebih banyak pembahasan soal-soal Persiapan UTBK (Penalaran Matematika) dapat anda baca di
kunjungi kak RH YT Channel : taklukan soal UTBK


