Koordinat titik puncak grafik fungsi kuadrat: Sumbu Simetri, Nilai Extrem Contoh 2 soal dan pembahasan

Koordinat titik puncak grafik fungsi kuadrat merupakan pertemuan persamaan sumbu simetri dengan nilai ekstrem fungsi baik pada titik balik minimum maupun titik balik maksimum. Untuk menentukan koordinat tersebut, kita bersama sama harus memahami bagaimana menentukan persamaan sumbu simetri (x) dan nilai extrem (y).

Daftar Isi

Sumbu Simetri

Sumbu simetri pada parabola merupakan garis imajiner yang membagi parabola menjadi dua bagian sama besar (simetris), perhatikan gambar!

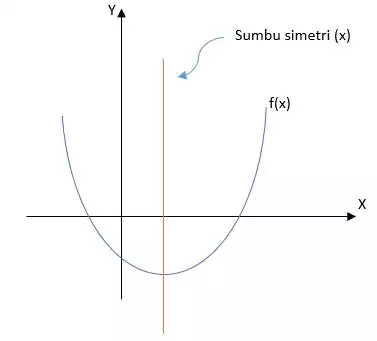
Persamaan sumbu simetri pada fungsi kuadrat $f(x)=ax^2+bx+c$ diperoleh dengan rumus

${\color{Blue}\textbf{x\;=\;-}\frac{\textbf{b}}{\textbf{2a}}}$

Nilai Extrem (y)

Nilai extrem fungsi kuadrat dicapai pada saat nilai domain x (sumbu simetri) disubtitusikan kedalam f(x) sehingga diperoleh f(x) = y dimana tidak terdapat nilai y lain yang lebih besar (nilai extrem maksimum) atau tidak terdapat nilai y lain yang lebih kecil (nilai extrem minimum). Nilai extrem fungsi kuadrat dapat dicari dengan formula

${\color{Blue}\textbf{y\;=\;-}\frac{\textbf{D}}{\textbf{4a}}}$

dengan D diskriminan fungsi kuadrat $f(x)=ax^2+bx+c$ diperoleh dengan

$D=b^2-4ac$

Koordinat Titik Puncak Fungsi Kuadrat

Dengan memperoleh persamaan sumbu simetri dan nilai extrem, titik puncak atau titik ektrem baik titik puncak minimum maupun titik puncak maksimum ditentukan dengan.

${\color{Blue}\textit{\textbf{(x,y)=}}\left(-\frac{b}{2a},-\frac{D}{4a}\right)=\left(-\frac{b}{2a},-\frac{b^2-4ac}{4a}\right)}$

Contoh Soal dan Pembahasan

Nomor 1

Koordinat titik puncak grafik fungsi kuadrat f(x)=2x²-8x+6 adalah….

A (2, -3)

B (3, -4)

C (4, -2)

D (5, -1)

E (6, -3)

Pembahasan

diketahui a = 2, b=-8 dan c=6

Persamaan sumbu simetri
$x=\frac{-b}{2a}=\frac{-(-8)}{2.1}=4$

Nilai optimum

$y=\frac{D}{-4a}=\frac{b^2-4ac}{-4.a}$

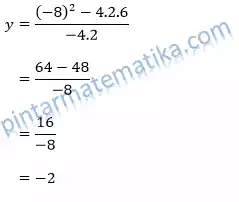
koordinat titik puncak

$\left(x,y\right)=\left(4,-2\right)$

Jawaban C

Nomor 2

Koordinat titik balik fungsi f(x)=3 – 2x – x² adalah

A (-2, 3)

B (-1, 4)

C (-1, 6)

D (1, -4)

E (2, -3)

Diketahui

$f(x)=-x^2-2x+3\;maka\;a=-1,\;b=-2,\;c=3$

Pembahasan

$\textrm{Koordinat\;titik\;balik}\;(x,y)=(-1,4)$

Jawaban B

Nomor 3

Koordinat titik puncak grafik fungsi kuadrat f(x)=x²+4x+3 adalah….

A (-2, -1)

B (-2, 3)

C (4, -2)

D (5, -1)

E (6, -3)

Pembahasan

diketahui a = 1, b=4 dan c=3

Persamaan sumbu simetri
$x=\frac{-b}{2a}=\frac{-4}{2.1}=-2$

Nilai optimum
$y=\frac{D}{-4a}=\frac{b^2-4ac}{-4.a}$
$y=\frac{4^2-4.1.3}{-4.1}$
$y=\frac{16-12}{-4}$
$y=\frac{4}{-4}=-1$

Koordinat titik puncak

$\left(x,y\right)=\left(-2,-1\right)$

Jawaban A

Untuk memperdalam materi diskriminan dapat diakses di

1 Rumus dan Sifat Diskriminan

2 Soal Soal terkait Diskriminan

Demikian ulasan mengenai Koordinat Titik Puncak Fungsi Kuadrat Contoh Soal dan pembahasannya, akan sangat bermanfaat untuk referensi persiapan seleksi masuk PTN PTS maupun Sekolah Kedinasan.

∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗

Untuk pengalaman belajar dan referensi belajar lebih banyak ada di

Pembahasan Soal Soal Matematika kelas 10

kunjungi kak RH YT Channel untuk menonton video pembahasan soal-soal matematika

Sumbu Simetri

Nilai Extrem (y)

Koordinat Titik Puncak Fungsi Kuadrat

Contoh Soal dan Pembahasan

Sebarkan ini:

Posting terkait: