Contoh Soal Aturan Sinus dan Cosinus
Pada kesempatan kali ini, kak RH akan membagikan contoh contoh soal Aturan Sinus dan Cosinus yang sering keluar, baik pada ulangan harian maupun pada ujian kenaikan kelas.
soal-soal yang kak RH upload ini juga merupakan soal latihan penalaran matematika untuk persiapan mengikuti SNBT UTBK bagi kelas 12.
Simak baik baik soal dan penmbahasan berikut ya.
Soal Nomor 1
Sebuah kapal berlayar ke timur. Dari pelabuhan kapal tersebut melihat mercusuar pada arah 30°. Setelah berlayar sejauh 12 km kapal tersebut melihat mercusuar yang sama pada arah 60°. Tentukan jarak mercusuar ke pelabuhan!
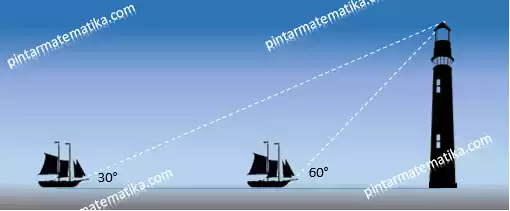
Pembahasan
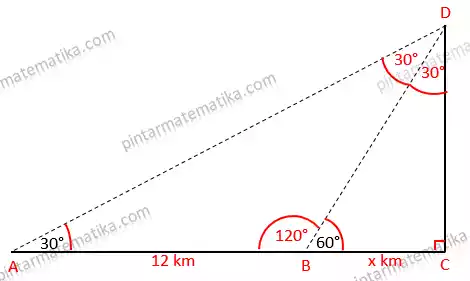
Ilustrasi gambar pada soal dapat dibuat sketsa sederhana sebagai berikut, dengan menambahkan titik D pada puncak mercusuar akan memudahkan perhitungan nantinya.
Pembahasan
Ilustrasi gambar pada soal dapat dibuat sketsa sederhana sebagai berikut, dengan menambahkan titik D pada puncak mercusuar akan memudahkan perhitungan nantinya.
Dari sketsa tersebut, pertama tama kita lengkapi beberapa komponen yang bias dilengkapi
- Perhatikan sudut ABD merupakan pelurus sudut CBD sehingga besar sudut ABD = 180 – 60 = 120
- Perhatikan segitiga ABD kedua sudutnya sudah diketahui sehingga dapat ditentukan besar sudut BDA = 180 – (120 + 30) = 180 – 150 = 30
- Perhatikan segitiga BCD kedua sudut sudutnya sudah diketahui sehingga dapat dihitung besar sudut BDC = 180 – (60 + 90) = 180 – 150 = 30
Untuk mencari jarak posisi A ke C atau AC terlebih dahulu dicari panjang BC atau x karena AC = AB + BC
Perhatikan segitiga ABD karena terdapat dua sudut sama besar (30°) maka segitiga ABD merupakan segitiga sama kaki dengan panjang AB sama dengan panjang BD yaitu 12 km.
Dengan menggunakan aturan sinus dapat dihitung jarak B ke C atau BC.
AC = AB + BC
AC = 12 + 6
AC = 18
Jadi jarak mercusuar (C) ke pelabuhan (kapal pada posisi A) adalah 18 km
Soal Nomor 2
Sebuah pesawat pengintai terbang dengan arah jurusan tiga angka 030° dan menempuh jarak 40 km. kemudian pilot membelokan arah pesawat sehingga pesawat menuju arah 090°. Pada arah yang baru pesawat menempuh jarak 80 km. tentukan jarak pesawat pesawat tersebut dari posisi awal (diketahui : √7=2,64 dan √3=1,73) !
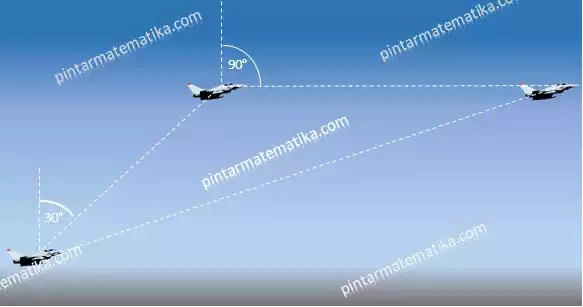
Pembahasan
Sebelum melakukan perhitungan jarak posisi pesawat terahir dari posisi awal, mari kita sederhanakan sketsa skema penerbangan sebagai berikut, missal posisi awal pesawat adalah P posisi kedua Q dan posisi ahir R, maka sketsa skema terbang dapat dibuat sebagai berikut.
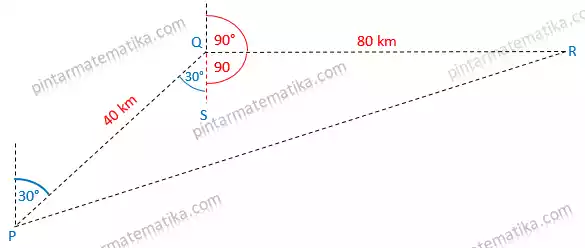
Berikutnya kita hitung besar sudut PQR, perhatikan garis putus putus vertical, sudut RQS merupakan pelurus dari sudut yang terbentuk pada belokan pesawat sehinnga besar sudut RQS = 90° sedangkan sudut PQS bertolak belakang dengan sudut pada permulaan pesawat sebesar 30°, sehingga besar sudut PQR = besar sudut RQS + besar sudut PQS = 120°.
Mari kita temukan jarak posisi awal pesawat pengintai (P) dengan posisi terahir (R) atau PR dengan menggunakan aturan cosinus.
Jadi jarak posisi awal pesawat pengintai dengan posisi terahir adalah 105,83 km
Soal Nomor 3
Kapal A dan B mengamati mercusuar C di tengah laut. Kapal A mengamati mercusuar dengan sudut elevasi 15° sedangkan kapal B mengamati dengan sudut elevasi 45°. Posisi kapal A dan B saling berseberangan dengan jarak 900 meter. Berapa jarak kapal A dengan puncak mercusuar C !
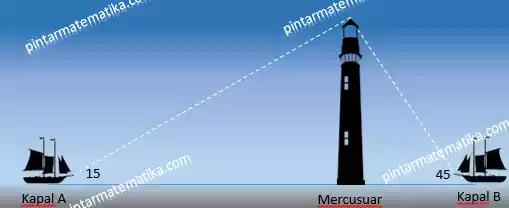
Pembahasan
Pertama tama mari sederhanakan dengan sketsa model gambar pada soal
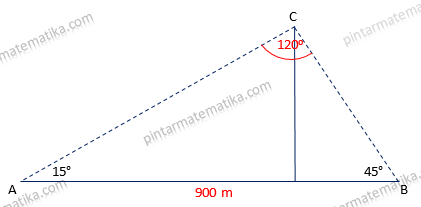
Dari sketsa diperoleh besar sudut ACB = 180 – (15+45) = 180 – 60 = 120
Ditanyakan berapa jarak kapal A dengan puncak mercusuar C atau panjang AC.
Maka permasalahan ini dapat diselesaikan dengan memanfaatkan aturan sinus
Jadi jarak kapal A sejauh 732 meter dari puncak mercusuar C
Soal Nomor 4
Diketahui segitiga ABC dengan besar sudut B = 30°, sudut C = 135° dan panjang AB = 36 cm. Tentukan unsur sisi-sisi dan sudut-sudut yang belum diketahui!
Pembahasan
Untuk mempermudah dalam menyelesaikan tipe soal soal seperti ini biasakan membuat sketsa ilustrasi gambar. Pada soal kali ini jelas kita akan membuat figure segitiga ABC dengan keterangan lengkap sesuai soal sebagai berikut
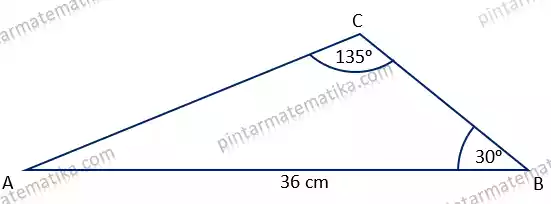
Untuk mencari panjang AC kita gunakan aturan sinus dengan sisi AC berpasangan dengan sudut B dan sisi AB dengan sudut C sebagai berikut
Soal Nomor 5
Sari dan Ani berdiri di pantai, mereka terpisah dengan jarak 6 km. Garis pantai berbentuk garis lurus keduanya dapat mengamati kapal laut yang sama dari tempat mereka berdiri. Sudut antara tempat Sari berdiri dengan kapal laun adalah 45°. Sementara, sudut antara tempat Ani berdiri dengan kapal laut tersebut adalah 15°. Tentukan jarak Ani dengan kapal !
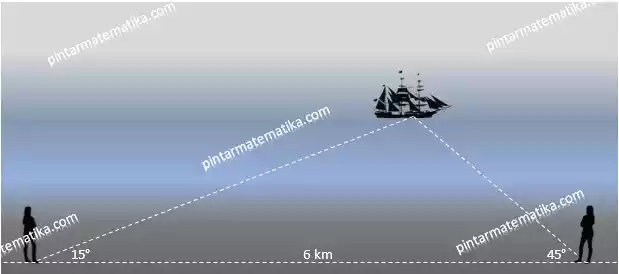
Pembahasan
Berikut adalah sketsa posisi kedua pengamat dengan kapal yang diamati. Missal Ani (A), Sari (S) dan Kapal (K) dengan jarak AS = 6 km
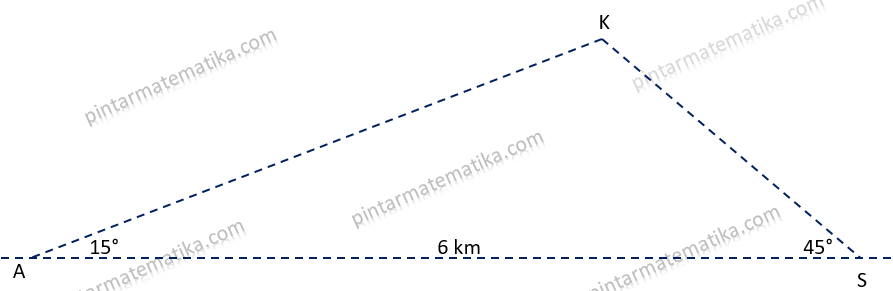
Jarak Ani (A) ke kapal (K) atau AK dapat dihitung dengan memanfaatkan aturan sinus, sisi AK berpasangan dengan sudut ASK akan sebanding dengan panjang sisi AB berpasangan dengan besar sudut AKS.
Untuk kelengkapan aturan sinus pertama tama dihitung besar sudut AKS atau sudu K = 180 – (A + S) = 180 – (15 + 45) = 180 – 60 = 120
maka perhitungannya adalah
Jadi jarak tempat Ani berdiri dengan Kapal yang diamati adalah 4,88 km atau 4880 m
Soal Nomor 6
Dua orang mengamati balon udara dari dua tempat yang berbeda seperti ilustrasi gambar berikut
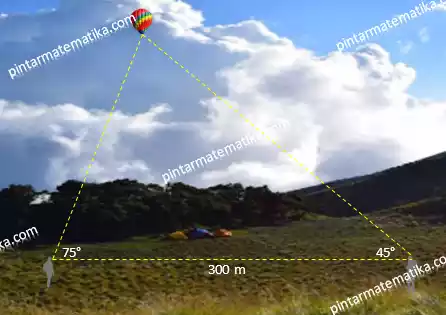
Diketahui jarak kedua pengamat adalah 300 meter, pengamat A mengamati balon dengan sudut elevasi sebesar 75° sedangkan sudut elevasi yang terbentuk antara pengamat B dengan balon adalah 45°. Jarak pengamat A terhadap balon udara adalah….
Pembahasan
sketsa sederhana dari ilustrasi pada soal adalah sebagai berikut
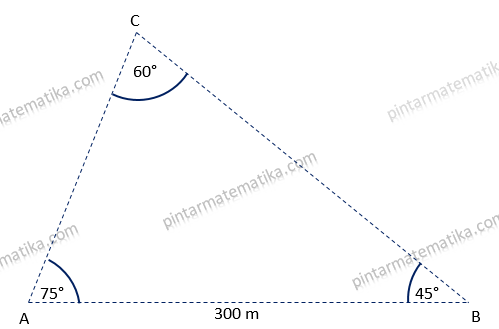
Dari sketsa tersebut terlebih dahulu dihitung besar sudut C
C = 180 – (A + B) = 180 – (75 + 45) = 180 – 120 = 60
Jarak pengamat A terhadap balon udara dapat dihitung dengan menggunakan aturan sinus sebagai berikut
Jadi Jarak pengamat A terhadap balon udara adalah 244 meter
Soal Nomor 7
Pak Hasan berpartisipasi dalam acara penghijauan pada area terbuka di sebuah camp area. Beliau akan menanam pohon manga pohon jambu dan pohon alpukat dengan posisi seperti ilustrasi berikut

Jarak pohon manga dan pohon jambu 6 meter, jarak pohon manga dengan pohon alpukat 10 meter sedangkan sudut yang terbentuk antara pohon Jambu Mangga Alpukat 120°. Hitunglah jarak pohon jambu dengan pohon alpukat, lengkap dengan caranya.
Pembahasan
Sketsa dari ilustrasi pada soal dengan J adalah pohon Jambu, M pohon mangga dan A pohon Alpukat dibuat sebagai berikut
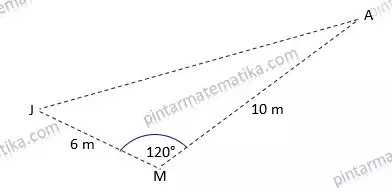
Setelah mengamati sketsa dengan seksama dimana diketahui dua buah panjang sisi segitiga mengapit satu sudut (dalam kasus inisebesar 120ᵒ), maka permasalahan tersebut dapat diselesaikan dengan menggunakan aturan cosinus.
Jadi jarak pohon jambu dengan pohon alpukat adalah 14 meter
Contoh Soal Serupa dari BAB Aplikasi Trigonometri KLIK DI SINI
*******
Lebih banyak pembahasan soal-soal Persiapan UTBK (Penalaran Matematika) dapat anda baca,
kunjungi kak RH YT Channel : taklukan soal UTBK untuk belajar hal hal menarik lainnya


