Bentuk Eksponen, Polar dan Rectangular Bilangan Kompleks disertai 10 contoh soal dan pembahasan

Daftar Isi

Definisi Bilangan Kompleks

Bilangan komplek, sahabat pintar sangat jarang sekali mendengar bilangan kompleks ketika masih di bangku sekolah dasar maupun sekolah menengah pertama. Pada waktu kelas 10 pernah suatu ketika mendapati masalah sebagai berikut

Tentukan nilai nilai x yang memenuhi persamaan x² + 1 = 0

Kemudian pada saat mencoba memecahkan masalah tersebut sobat pintar menemukan bentuk yang lumayan menyulitkan

$\begin{matrix}x^2+1=0\;\;\;\;\;\\\;\;\;\;x^2=-1\\\;\;\;\;\;\;\;\;\;x=\sqrt{-1}\\\end{matrix}$

Sampai disini mentok, bagaimana bisa akar bilangan negative diselesaikan? Lalu pegang kalkulator dan ketika menghitung akar negative satu hasilnya “error”.

Usut punya usut rupanya bentuk bilangan kompleks memegang peran penting dalam penyelesaian masalah di atas. Bagaimana?

Mari kita mulai dari memahami bahwa bilangan komplek yang sedang kita bicarakan memiliki symbol z dimana merupakan gabungan bilangan riil dan bilangan imajiner ( i ) dimana i = √(-1).

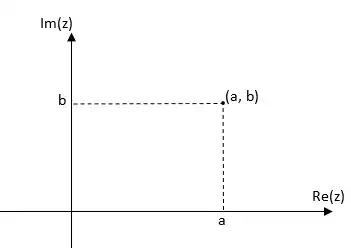
Secara umum bilangan imajiner dituliskan sebagai z = a + bi,

pada penulisan geometri z dinyatakan dengan z = x + yi

sering dituliskan dalam pasangan berurut z (x , y)

x merupakan bagian riil dari bilangan Z dinotasikan x = Re(z)

y merupakan bagian imajiner dari bilangan Z dinotasikan y = Im(z)

Bilangan kompleks z = x + yi dapat digambarkan dalam diagram kartesius dengan x pada sumbu horizontal selanjutnya disebut dengan sumbu riil dan y pada sumbu vertical disebut sumbu imajiner. Istilah untuk bidang yang digunakan menggambar bilangan kompleks disebut bidang kompleks atau bidang argand.

Bentuk Bentuk Bilangan Kompleks

Bilangan kompleks dapat dituliskan dalam berbagai bentuk yaitu:

1 Bentuk Rectangular

2 Bentuk Polar dan

3 Bentuk Eksponensial

Bentuk Rectangular

z = a + bi atau z = x + yi digambarkan dalam bidang kompleks dengan a atau x sebagai absis dari sumbu riil dan y merupakan ordinat mewakili sumbu imajiner,

Bentuk Polar

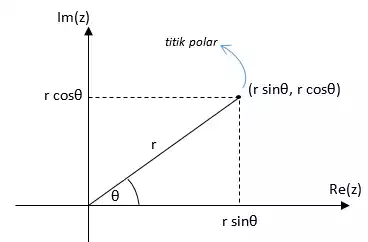
Bentuk z = r (cos θ + i sin θ)

Dimana r merupakan radius atau jarak terhadap titik polar dari titik asal r diperoleh dengan

r² = x² + y²

sedangkan besar sudut ( θ ) diperoleh dari arces tangen pada gradient r itu sendiri, secara matematis

m = tanθ = b/a sehingga θ = Arc tan(b/a) atau

$\theta=Arc\left(\frac{sin\frac{b}{a}}{cos\frac{b}{a}}\right)$

Selanjutnya θ dapat diperoleh dengan memanfaatkan perbandingan trigonometri selain tangen

$\begin{matrix}\theta=Arc\;cos\left(\frac{x}{r}\right)\\atau\\\theta=Arc\;sin\left(\frac{y}{r}\right)\\\end{matrix}$

Digambarkan dalam bidang argand sebagai

Bentuk Eksponensial

Selain Rectangular dan Polar, bilangan kompleks dapat dituliskan dalam Bentuk Eksponensial

z = re^iθ

r dan θ diperoleh dengan langkah yang sama seperti ketika mengubah bentuk rectangular ke bentuk polar.

Okay sobat Pintar, dari penjelasan di atas, soal Tentukan nilai nilai x yang memenuhi persamaan x² + 1 = 0 tidak lagi berkendala, sudah tahu kan berapa nilai √(-1) ?

Contoh Soal dan Pembahasan

Nomor 1

Bentuk eksponen bilangan kompleks z=√3+i adalah….

Pembahasan

Untuk menentukan bentuk eksponen $\left(z=re^{i\theta}\right)$ suatu bilangan kompleks $\left(z=x+iy\right)$

terlebih dahulu dihitung nilai θ

diketahui x = √3 dan y = 1

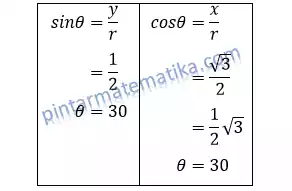
$\begin{matrix}r=\sqrt{x^2+y^2}\;\;\;\;\;\;\;\\\\=\sqrt{\sqrt{3}^2+1^2}\\\\=\sqrt{4}\;\;\;\;\;\;\;\;\;\;\;\;\;\\\\=2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\end{matrix}$

dengan demikian, bentuk eksponen dari bilangan kompleks tersebut adalah

$\begin{matrix}z=re^{i\theta}\\\\=2e^{i30}\\\end{matrix}$

Nomor 2

Bentuk polar dari bilangan kompleks z $=1+\sqrt{3}\;i$ adalah….

Pembahasan

Diketahui $x=1\;\textrm{dan}\;\;y=\sqrt{3}$

$\begin{matrix}r=\sqrt{x^2+y^2}\;\;\;\;\;\;\\\\=\sqrt{1^2+\sqrt{3}^2}\\\\=\sqrt{4}\;\;\;\;\;\;\;\;\;\;\;\;\;\\\\=2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\end{matrix}$

$\begin{matrix}cos\theta=\frac{x}{r}\;\;\;\;\;\;\;\;\\\\=\frac{1}{2}\\\\\theta=60^\circ\\\end{matrix}$

$\begin{matrix}sin\theta=\frac{y}{r}\;\;\;\;\;\;\;\;\\\\=\frac{\sqrt{3}}{2}\\\\\theta=60^\circ\\\end{matrix}$

Bentuk polar

$\begin{matrix}z=r(cos\theta+i\;sin\theta)\;\;\;\;\;\;\\=2(cos60+i\;sin60)\\\end{matrix}$

Nomor 3

Bentuk eksponen bilangan kompleks berikut z=1+i adalah….

Pembahasan

Untuk menentukan bentuk eksponen $\left(z=re^{i\theta}\right)$ suatu bilangan kompleks $\left(z=x+iy\right)$

terlebih dahulu dihitung nilai θ

diketahui x=1 dan y=1

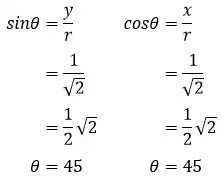
$\begin{matrix}r=\sqrt{x^2+y^2}\;\;\\\\=\sqrt{1^2+1^2}\\\\=\sqrt{2}\;\;\;\;\;\;\;\;\;\\\end{matrix}$

dengan demikian, bentuk eksponen dari bilangan kompleks tersebut adalah

$\begin{matrix}z=re^{i\theta}\;\;\;\;\;\;\;\\\\=\sqrt{2}e^{i45}\\\end{matrix}$

Nomor 4 dan Nomor 5

Tentukan bentuk polar dari bilangan kompleks berikut

$4.\;\;\;z=2+2i$

$5.\;\;\;z=\sqrt{3}+i$

Pembahasan

4. diketahui x = 2 dan y = 2

$r=\sqrt{x^2+y^2}$

$=\sqrt{2^2+2^2}$

$=\sqrt{8}$

$=2\sqrt{2}$

θ = 45º

Jadi, bentuk polar dari bilangan kompleks $z=2+2i$ adalah

$z=r(cos\theta+isin\theta)$

$z=\frac{1}{2}(cos45+isin45)$

5. Diketahui $x=\sqrt{3}\;\;\textrm{dan}\;\;y=1$

$r=\sqrt{x^2+y^2}$

$=\sqrt{(\sqrt{3})^2+1^2}$
$=\sqrt{4}$
$=2$

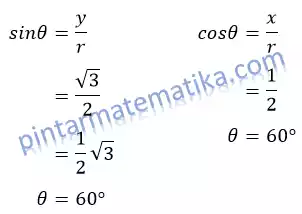
Jadi, bentuk polar dari bilangan kompleks $z=\sqrt{3}+i$ adalah

$z=r(cos\theta+i\;sin\theta)$

$z=2(cos60+i\;sin60)$

Nomor 6 sampai 9

Tentukan bagian real dan imajiner dari bilangan kompleks berikut:

$6.\;3+i$

$7.\;3-\sqrt{-9}$

$8.\;\sqrt{3}$

$9.\;\sqrt{(-3)^3}$

Pembahasan

6. Bentuk 3 + i atau 3 + 1i memiliki dua bagian yaitu 3 adalah bagian real dan 1 adalah bagian imajiner

7. Bentuk $3-\sqrt{-9}$ dapat ditulis sebagai

$\begin{matrix}3-\sqrt{-9}=3-\sqrt{9i}\;\;\;\;\;\;\;\;\;\;\;\;\\=3-3i\\\end{matrix}$

bagian real = 3
bagian imajiner = -3

8. $\sqrt{3}$ dapat dipandang sebagai bilangan kompleks dengan dinyatakan sebagai $\sqrt{3}+0i$

bagian real = $\sqrt{3}$
bagian imajiner = 0

9. $\sqrt{(-3)^3}$ dapat dinyatakan sebagai bilangan kompleks dengan bentuk sebagai berikut

$\begin{matrix}\sqrt{(-3)^3}=0+\sqrt{(-3).(-3).(-3)}\\=0+3\sqrt{(-3)}\;\;\\=0+3\sqrt{3}i\;\;\;\;\;\;\;\\\end{matrix}$

bagian real = 0
bagian imajiner = $3\sqrt{3}$

Nomor 10

Bentuk rectangular dari bilangan kompleks $z=-\frac{9+\sqrt{-9}}{3}$ adalah…

Pembahasan

$\begin{matrix}z=\frac{9+\sqrt{-9}}{3}\\\\z=\frac{9+\sqrt{9i}}{3}\\\\z=\frac{9+3\sqrt{i}}{3}\\\\z=3+3\sqrt{i}\\\end{matrix}$

*******

Lebih banyak pembahasan soal-soal Persiapan UTBK (Penalaran Matematika) dapat anda baca di

kunjungi kak RH YT Channel : taklukan soal UTBK

Semoga bermanfaat.

Definisi Bilangan Kompleks

Bentuk Bentuk Bilangan Kompleks

Bentuk Rectangular

Bentuk Polar

Bentuk Eksponensial

Contoh Soal dan Pembahasan

Sebarkan ini:

Posting terkait: