Barisan Aritmatika
Barisan Aritmatika terdiri atas suku suku dimana selisih antar suku selalu sama, sehingga selisih suku kedua dengan suku pertama sama dengan selisih suku ketiga dengan suku kedua, sama dengan selisih suku keempat dengan suku ketiga dan seterusnya bilangan selisih antar suku ini kemudian disebut dengan beda barisan aritmatika.
Suku pertama barisan aritmatika disimbolkan dengan huruf a, sedangkan suku kedua merupakan hasil dari suku pertama ditambah dengan beda barisan dan seterusnya untuk suku suku berikutnya. Perhatikan pola berikut:
U1 = a
U2 = a + b
U3 = (a + b) + b = a + 2b
U4 = (a + 2b) +b= a + 3b
dari pola tersebut dapat diamati bahwa untuk setiap suku ke-n diperoleh menggunakan pola menambah a dengan (n – 1)b sehingga dapat dituliskan
Un = a + (n-1)b
dengan b = Un – U(n-1)
Barisan aritmatika dengan suku ganjil, akan memiliki suku tengan (Ut), dimana suku tengah dapat diperoleh dengan
Ut = ½ (a + Un)
Deret aritmatika
Suku suku pada barisan aritmatika dapat dijumlahkan sebagian atau keseluruhan, jumlah n suku pertama pada barisan aritmatika disebut dengan deret hitung aritmatika selanjutnya disimbolkan dengan Sn
Sn = U1 + U2 + U3 + U4 +…+ Un
Sn = a + (a+b) + (a+2b) + (a+3b) + … + a+(n-1)b
Secara singkat jumlah n suku pertama deret aritmatika dapat dihitung dengan rumus
Contoh Soal dan Pembahasan
Nomor 1
Suatu barisan aritmatika diketahui suku ke 6 adalah -4, sedangkan jumlah suku ketiga dan kelima adalah 4. tentukan :
- Beda barisan dan suku pertama
- Rumus suku ke-n
- Suku ke-21
Diketahui
Pembahasan
Pertanyaan A. Beda barisan dan suku pertama

Pertanyaan B. Rumus suku ke-n
Pertanyaan C. Suku ke-21
Nomor 2
Diketahui barisan aritmatika dengan suku dan suku
Tentukan suku pertama, beda barisan dan rumus suku ke-n barisan tersebut !
Pembahasan
Diketahui
ingat bahwa rumus umum suku ke-n barisan aritmatika
sehingga
Eliminasi persamaan 1 dan persamaan 2
jika persamaan 1 dikurangi persamaan 2 akan diperoleh
mencari nilai a dari salah satu persamaan
Rumus suku ke-n barisan tersebut diperoleh dengan cara
Nomor 3
Suatu perusahaan pada tahun-tahun pertama memproduksi 5000 unit barang. pada tahun-tahun berikutnya produksi turun secara tetap. jika pada tahun ke-6 memproduksi 4600 unit barang, pada tahun keberapa perusahaan tersebut memproduksi 3000 unit barang?
Diketahui
ditanyakan n
Pembahasan
mari kita mulai dengan mencari beda (b)
mencari banyak suku (n)
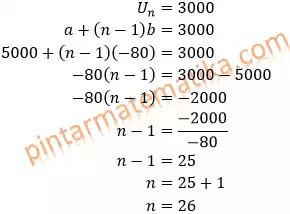
jadi perusahaan akan memproduksi 3000 unit barang pada tahun ke 26
Nomor 4
Berdasarkan data pada bulan Januari 2022 perusahaan A mampu menjual 8 sepeda motor. Pada bulan Februari dan Maret perusahaan A mampu menjual masing-masing 15 dan 22 sepeda motor Apabila relasi antara bulan dan jumlah penjualan sepeda motor membentuk fungsi linear, tentukan penjualan sepeda motor pada bulan Agustus!
Pembahasan
Cara 1

misal januari adalah suku pertama (a=8) februari merupakan suku kedua (U2=15) maret suku ketuga dan seterusnya diperlihatkan pola bahwa penjualan sepeda motor setiap bulan membentuk barisan aritmatika dengan beda (b=15-8=7) sehingga agustus adalah suku ke delapan
cara II

Selanjutnya, kita dapat menggunakan titik pertama (Januari) untuk mencari c (konstanta)
jadi
penjualan bulan Agustus (bulan ke 8)
Jadi, perkiraan penjualan sepeda motor pada bulan Agustus adalah 57 unit.
Nomor 5
Sari naik taksi dari kota A ke kota B yang berjarak 8 kilometer. Besar argo taksi adalah Rp 7.000,00 untuk 1KM pertama, kemudian bertambah Rp600,00 tiap 100 meter selanjutnya. Besarnya ongkos taksi yang harus dibayar sari adalah….
Pembahasan
Perhatikan skema jarak tempuh berikut

dengan demikian dapat dituliskan banyaknya suku barisan aritmatika adalah
n = 1 + 70 = 71
dengan a = 7 000 dan b = 600
jadi, besar ongkos taksi yang harus dibayar Sari Rp49.000,-
Nomor 6
Jumlah semua bilangan asli diantara 5 dan 115 yang habis dibagi 2 tetapi tidak habis dibagi 3 adalah…
Bilangan antara 5 dan 115 yang habis dibagi 2
6,8,10,12,…114
Bilangan antara 5 dan 115 yang habis dibagi 2 juga habis dibagi 3
6,12,18,24,…,114
sehingga jumlah bilangan asli diantara 5 dan 115 yang habis dibagi 2 tetapi tidak habis dibagi 3 adalah
Nomor 7
Dalam suatu gedung terdapat 30 baris kursi. Banyak kursi pada baris pertama ada 20 kursi, baris kedua 24 kursi, baris ketiga ada 28 kursi dan seterusnya dengan beda yg sama. Tentukan banyak kursi dalam gedung tersebut !
Diketahui
Pembahasan
jadi terdapat 2340 kursi dalam gedung tersebut
Demikian paparan materi Barisan dan deret Aritmatika beserta contoh aplikasi soal dan pembahasanya
Materi dan contoh soal Barisan Geometri dapat dibaca DISINI
Contoh soal dan aplikasi barisan dan deret dalam kasus sehari jari dapat dibaca DISINI
Materi ini akan sangat bermanfaat sebagai referensi belajar persiapan ASAS, Ujian Sekolah dan Persiapan Seleksi Masuk Perguruan Tinggi atau UTBK SNBT
Lebih banyak pembahasan soal-soal dapat anda baca di Persiapan UTBK (Penalaran Matematika)
kunjungi kak RH YT Channel : taklukan soal UTBK




