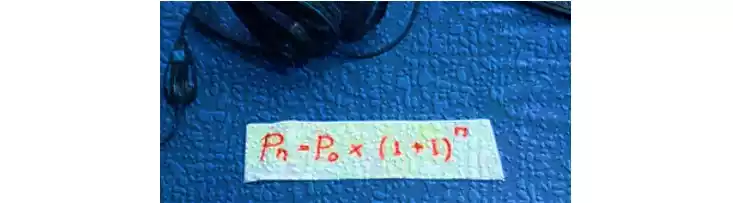Fungsi Pertumbuhan Eksponen : Banyak penduduk suatu kota setiap tahun mengalami kenaikan (pertambahan nilai) sebesar 1%

Daftar Isi

Fungsi Pertumbuhan Eksponen

Pertumbuhan Eksponen diartikan sebagai kenaikan nilai suatu besaran seiring waktu terus meningkat.

Contoh kasus pertumbuhan diantaranya : bunga majemuk, pertumbuhan penduduk, perkembangan bakteri dan atau virus.

Secara umum fungsi pertumbuhan eksponen dirumuskan sebagai

$P_n=P_o\times a^n$ atau $P_n=P_o\times(1+i)^n$

dengan :

P_n= Nilai besaran setelah n periode waktu

P_o = Nilai besaran pada awal periode atau nilai besaran mula mula

a = disebut sebagai faktor pertumbuhan, a = (1 + i) dimana i laju pertumbuhan, a > 1

n = besar periode pertumbuhan

Untuk lebih memahami, mari perhatikan contoh berikut:

Contoh Soal dan Pembahasan

Nomor 1

Banyaknya penduduk di suatu kota setiap tahun mengalami kenaikan 1% dari total penduduk dari tahun sebelumnya. Menurut sensus penduduk tahun 2010 penduduk di kota tersebut sebanyak 200000 orang. Jumlah penduduk pada tahun 2030 adalah….

A. 225023 jiwa

B. 229005 jiwa

C. 234056 jiwa

D. 237085 jiwa

E. 244038 jiwa

Pembahasan

permasalahan pada nomor 5 merupakan masalah pertumbuhan eksponen, dimana kuantitas atau jumlah akan terus meningkat selama interval waktu tertentu dengan prosentase kenaikan yang tetap.

untuk menyelesaikan masalah ini dapat digunakan rumus pertumbuhan eksponensial sebagai berikut:

$P_n=P_o\times(1+i)^n$

dengan Pn adalah populasi dalam waktu n periode, Po merupakan populasi awal dan i sebagai laju pertumbuhan sesuai periode waktu tertentu.

pada soal di atas, diketahui :

prosentase pertumbuhan sebesar 1% atau i=1% = 0,01 per tahun dengan demikian faktor pertumbuhan a = (1 + 0,01)

populasi awal (populasi penduduk tahun 2010) = 200000 jiwa

periode n dihitung dari 2010 sampai 2030 sehingga n = 20 tahun

Perhitungan Populasi pada tahun ke 20 atau P20 sebagai berikut

$\begin{matrix}P_n=P_o\times(1+i)^n\;\;\;\;\;\;\;\;\;\;\;\;\;\\P_{20}=200000\times(1+0,01)^{20}\\=200000\times(1,01)^{20}\\=200000\times 1,22019\\=244038\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\end{matrix}$

jadi pada tahun 2030 terdapat 244038 jiwa penduduk

Jawaban E

Nomor 2

Pada sebuah pengamatan perkembangan bakteri, diamati sebanyak 500 bakteri. Bakteri membelah menjadi dua setiap 20 menit. Berapa jumlah bakteri setelah 2 jam adalah….

A. 8000

B. 12264

C. 16200

D. 28000

E. 32000

Pembahasan

dengan Pn adalah populasi dalam waktu n periode, Po merupakan populasi awal dan a sebagai faktor pertumbuhan sesuai periode waktu tertentu. Dari soal di atas dapat diketahui:

Populasi awal atau Po = 500

Periode pertumbuhan n = 1 jam ÷ 20 menit = 120 ÷ 20 = 6

Faktor pertumbuhan a = 2

Jadi jumlah bakteri setelah 2 jam sebanyak

$\begin{matrix}P_n=P_o\times a^n\;\;\;\;\;\;\\=500\times 2^6\\=500\times 64\\\;\;\;\;\;\;\;=32000\;\textrm{bakteri}\\\\\end{matrix}$

Jawaban E

Nomor 3

Banyak penduduk suatu kota setiap tahun mengalami kenaikan sebesar 1% dari jumlah penduduk tahun sebelumnya. Berdasarkan sensus penduduk tahun 2020, penduduk dikota tersebut sebanyak 200.000 orang. Perkiraan jumlah penduduk pada tahun 2040 adalah….

231500
237820
242440
244038
251500

Pembahasan

Dengan Pn adalah populasi dalam waktu n periode, Po merupakan populasi awal dan i sebagai laju pertumbuhan sesuai periode waktu tertentu.

pada soal di atas, diketahui :

prosentase pertumbuhan sebesar 1% atau i=1% = 0,01 per tahun dengan demikian faktor pertumbuhan a = (1 + 0,01)

populasi awal (populasi penduduk tahun 2020) = 200000 jiwa

periode n dihitung dari 2020 sampai 2040 sehingga n = 20 tahun

Jumlah penduduk pada tahun 2040 adalah

Jawaban D

Nomor 4

Seekor amoeba berkembang biak dimana jumlahnya mengikuti fungsi $A_t=A_0\times 2^t$ dengan t (menit) adalah waktu yang dibutuhkan amoeba untuk berkembang biak. Jika pada pukul 10.15 terdapat 100 amoeba, pukul berapa banyak amoeba menjadi 18100 ? (log 181 = 2,2577 dan log2 = 0,3010)