Komposisi Fungsi
Komposisi fungsi f(x) dan g(x) atau misalkan kita tulis sebagai h(x) dimana f(x) dikerjkan terlebih dahulu kemudian dilanjutkan g(x) biasa disimbolkan dengan (g o f)(x) dalah hal ini ditulis h(x) = (g o f)(x), sehingga h(x) merupakan fungsi tunggal yang selanjutnya disebut sebagai fungsi komposisi.
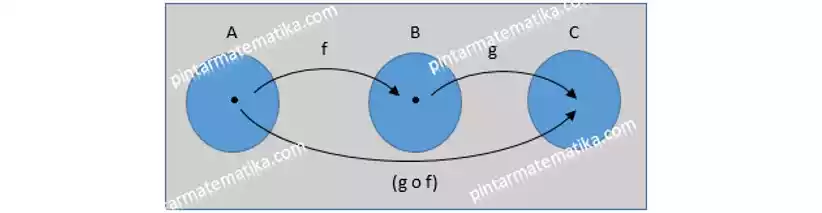
Sederhananya begini, Jika fungsi f memetakan A ke B dan fugsi g memetakan B ke C maka komposisi fungsi f dan g dituliskan (g o f) akan memetakan A ke C.
Gambar yang mewakili fungsi komposisi f dan g seperti penjelasan diatas, sebagai berikut
Contoh soal dan pembahasan
Nomor 1
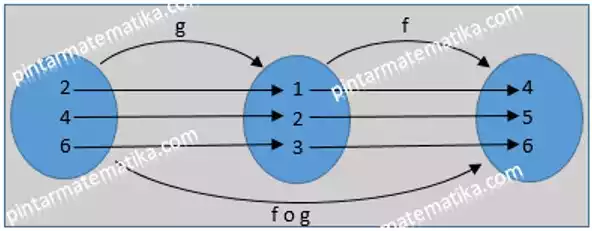
Diketahui fungsi f memetakan x ke y dengan f = {(1,4), (2,5), (3,6)} dan fungsi g memetakan y ke z dengan g={(2,1), (4,2), (6,3)} tentukan hasil adri fungsi komposisi (f o g) !
A 1, 2, 3
B 2, 4, 6
C 4, 5, 6
D 3, 6, 9
E 5, 7, 9
Pembahasan
(f o g) berarti fungsi g dilanjutkan oleh fungsi f, artinya range atau hasil dari fungsi g merupakan daerah asal dari fungsi f sehingga diperoleh
(f o g)(2) = f(g(2)) = f(1) = 4
(f o g)(4) = f(g(4)) = f(2) = 5
(f o g)(6) = f(g(6)) = f(3) = 6
Kalau disajikan dalam diagram panah sebagai berikut
Jawaban C
Nomor 2
Fungsi f dan fungsi g ditentukan oleh f(x) = 3 – x dan g(x) = x² + 5. Komposisi fungsi (f o g)(x) adalah…
A x² – 2
B x² + 2
C -x² – 2
D -2x² + 1
E 2x² – 1
Pembahasan
(f o g)(x) = f(g(x))
= f(x² + 5)
= 3 – (x² + 5)
= 3 – x² – 5
= – x² – 2
Jawaban C
Nomor 3
Diketahui fungsi f(x) = 2x² – 3x + 1 dan fungsi g(x) = 4x – 2 tentukan nilai dari (f o g)(-2) adalah….
A 231
B 179
C -130
D -245
E -330
Pembahasan
(f o g)(-2) = f(g(-2))
Akan menjadi lebih mudah apabila kita hitung terlebih dahulu hasil dari g(-2) sebagai berikut
g(x) = 4x – 2
g(-2) = 4(-2) – 2
g(-2) = -8 – 2
g(-2) = -10
Sehingga f(g(-2)) dapat dihitung sebagai berikut
f(x) = 2x² – 3x + 1
f(g(-2)) = 2(g(-2)) ² – 3(g(-2)) + 1
f(-10) = 2(-10) ² – 3(-10) + 1
f(-10) = 200 + 30 + 1
f(-10) = 231
sehingga (f o g)(-2) = 231
Jawaban A
Nomor 4
Pendapatan dari penjualan suatu produk adalah R(x) = 5x² + 1000 x, sedangkan biaya produksi C(x) adalah 50x + 6000 dengan x menyatakan jumlah produksi. keuntungan yang diperoleh pada setiap penjualan 10 pruduk adalah….
A 3000
B 3600
C 4000
D 4350
E 5000
Pembahasan
Misal keuntungan sebagai fungsi dari jumlah produk x = k(x)
maka berlaku
K(x) = R(x) – C(x)
= (5x² + 1000x) – (50x + 6000)
= 5x² + 1000x – 50x – 6000
= 5x² + 950x – 6000
K(10)= 5(10)² + 950(10) – 6000
=500 + 9500 – 6000
=4000
Jawaban D
Nomor 5
Diketahui f(x)= x – 3 dan g(x)=x² – 3x +2. Salah satu nilai a yang memenuhi (g o f)(a)=6 adalah….
A 1
B 2
C 3
D 4
E 5
Pembahasan
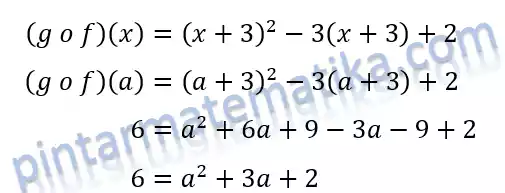
Jawaban A
Nomor 6
Nilai (f o g)(x) untuk x = -6 apabila f(x) = x²+4x – 5 dan adalah….
A -6
B -5
C 3
D 5
E 6
Pembahasan

Jawaban B
Demikian paparan materi komposisi fungsi beserta contoh soal dan pembahasannya dapat dijadikan referensi belajar.
Lebih banyak pembahasan soal-soal Matematika Kelas XI dapat anda baca dan
kunjungi kak RH YT Channel : taklukan soal UTBK untuk belajar hal hal menarik lainnya
Semoga bermanfaat.