Teorema Bayes dan peluang kejadian marginal memiliki keterkaitan yang erat, sebelum masuk pada rumus dan penggunaan teorema Bayes akan dibahas terlebih dahulu mengenai peluang kejadian marginal.
Peluang Kejadian Marginal Sebagai bagian dari teorema bayes
Suatu ketika anda mengikuti sebuah permainan mengambil sebuah bola berwarna dari salah satu gelas (cup) terbalik dari tiga cup yang diacak di atas meja. Di dalam cup cup yang disediakan diisi bola merah dan putih atau merah saja atau putih saja.
Pertama tama cup diacak dan anda diminta memilih satu dari tiga cup. Dengan mata tertutup anda diminta mengambil satu bola yang ada di dalamnya, permainan berahir kemenangan ketika orang tersebut mampu menebak warna bola yang terambil
Nah teman teman, permainan tersebut sebenarnya terdapat peluang peluang yang dipengaruhi peristiwa peristiwa pada prosesnya. Probabilitas atau peluang suatu peristiwa yang diperoleh dari peluang peluang gabungan disebut sebagai Probabilitas Marginal atau Peluang Marginal.
Dari contoh game di atas missal Cup pertama kita sebut A1, cup kedua disebut A2 dan cup ketiga adalah A3 merupakan kejadian saling lepas pada seluruh kemungkinan pemilihan ( ruang sampel S) dan kejadian terambilnya salah satu bola berwarna pada permainan tersebut kita sebut B dalam ruang sampel S yang sama. Maka peluang Marginal atau Marginal Probability dapat dihitung dengan rumus
P(B) = P(B/A1). P(A1) + P(B/A2). P(A2) + P(B/A3). P(A3)
Rumus umum Peluang Marginal
Keterangan :
P(B), peluang terjadinya kejadian B
P(B|Ai), Peluang terjadinya kejadian B setelah peristiwa Ai
P(Ai), peluang terjadinya peristiwa Ai
I = 1, 2, 3, 4,…
Teorema Bayes
Pada tahun 1763, seorang ahli statistik berkebangsaan Inggris bernama Thomas Bayes mengemukakan sebuah teorema yang kemudian dia namakan dengan Teorema Bayes.
Teorema Bayes yang dikenal juga dengan Aturan Bayes menyatakan seberapa besar perubahan kepercayaan seseorang dalam keadaan rasional atau secara rasional terhadap suatu hal ketika ditemukan fakta baru berupa petunjuk atau informasi akurat terkini. Teorema ini dianggap sebagai dasar pendekatan inferensi statistik khusus yang disebut inferensi Bayes.
Dalam statistic dan teori peluang (probabilitas), terdapat istilah peluang bersyarat dimana informasi tertentu yang diperoleh dari suatu peristiwa digunakan untuk memperkirakan probabilitas peristiwa yang lain. Dapat dikatakan terjadi revisi nilai peluang pada suatu peristiwa berdasarkan perubahan informasi atau fakta terbaru yang muncul atau probabilitas mengalami perubahan akibat fakta baru yang muncul.
Rumus Teorema Bayes
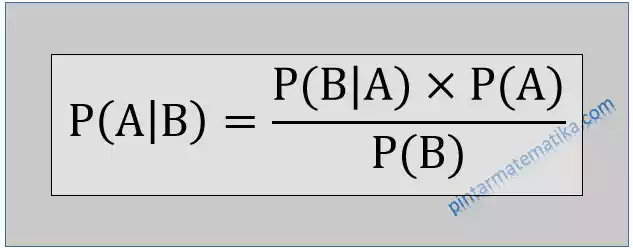
Keterangan rumus:
P(A|B) besar peluang terjadinya peristiwa A apabila peristiwa B sudah terjadi
P(B|A) besar peluang terjadinya peristiwa B apabila peristiwa A sudah terjadi
P(A) besar peluang suatu kejadian A
P(B) besar peluang suatu kejadian B
Soal dan Pembahasan
Soal No 1
Pada suatu ruang yang gelap terdapat tiga buah kotak tertutup, masing masing kotak berisi tiruan bola golf berlapis perak dan emas. Kotak pertama berisi 3 bola berlapis perak dan 2 bola berlapis emas, kotak kedua berisi satu bola berlapis perak dan empat bola berlapis emas sedangkan kotak ketiga berisi sebuah bola berlapis perak dan sebuah bola berlapis emas.
Anda mendapat keberuntungan untuk mengikuti game mengambil satu bola dari dalam ruang tersebut dengan aturan main sebagai berikut:
• Pertama tama anda diminta memasuki ruang gelap tersebut dan memilih satu kotak dari tiga kotak tersedia yang telah diacak posisinya.
• Setelah anda memilih salah satu kotak, dari kotak terpilih anda diminta mengambil satu bola dengan keadaan mata tertutup.
• Beberapa waktu setelah mengambil bola, anda dipersilakan membuka penutup mata dan ternyata yang anda ambil adalah bola berlapis emas.
Berapakah peluang bola yang sudah anda ambil tersebut terambil dari kotak pertama?
Pembahasan
Mari tentukan terlebih dahulu notasi yang dibutuhkan, missal
A₁ peristiwa terambil kotak pertama
A₂ peristiwa terambil kotak kedua
A₃ peristiwa terambil kotak ketiga
B adalah peristiwa terambil tiruan bola golf berlapis emas
B|Aᵢ peristiwa terambil bola golf berlapis emas pada kotak ke-i dengan i = 1, 2, 3
Peluang pemilihan kotak
Peluang Peristiwa terambil bola golf berlapis emas pada masing masing kotak
• Kotak pertama berisi 3 bola berlapis perak dan 2 bola berlapis emas
• Kotak kedua berisi satu bola berlapis perak dan empat bola berlapis emas
• Kotak ketiga berisi sebuah bola berlapis perak dan sebuah bola berlapis emas
Peluang marginal peristiwa terambil tiruan bola golf berlapis emas dari peristiwa tersebut atau P(B) dihitung dengan cara
Ditanyakan peluang terambil bola golf berlapis emas dari kotak pertama atau P(A₁|B)
Maka,
Jadi peluang terambilnya pada kotak pertama adalah 4/17
Soal No 2
Suatu penerbangan regular memiliki peluang berangkat tepat pada waktunya adalah 0.83, peluang penerbangan tersebut mendarat tepat pada waktunya adalah 0.94, dan peluang penerbangan itu berangkat dan mendarat pada waktunya adalah 0.77.
Hitunglah peluang pesawat pada penerbangan itu mendarat tepat waktu bila diketahui bahwa pesawat tersebut berangkat tepat waktu
Pembahasan
Notasi yang dibutuhkan:
A peristiwa berangkat tepat waktu
B peristiwa mendarat tepat waktu
(A ∩ B) peristiwa berangkat dan pulang tepat waktu
Diketahui
P(A) = 0.83
P(B) = 0,94
P(A ∩ B) =0,77
peluang pesawat pada penerbangan itu mendarat tepat waktu P(B) bila diketahui bahwa pesawat tersebut berangkat tepat waktu P(A) atau P(B|A)
jadi peluang pesawat pada penerbangan itu mendarat tepat waktu jika berangkat tepat waktu adalah 0,93
Soal No. 3
Dalam pemilihan ketua komunitas supporter team basketball suatu sekolah terdapat tiga calon ketua, Adam, Dhanu dan Shinta. Peluang masing-masing kandidat terpilih menjadi ketua 0.3, 0.4 dan 0.2.
Dalam sosialisasi pencalonan ketua ditemukan fakta siapapun yang terpilih akan terjadi kenaikan iuran anggota sebagai program berkelanjutan dari kepemimpinan sebelumnya. Peluang kenaikan iuran jika komunitas diketuai Adam sebesar 0,4 sedangkan Dhanu sebesar 0,6 dan Shinta sebesar 0,5.
Berapa peluang terjadinya kenaikan iuran anggota?
Penyelesaian :
Notasi yang dibutuhkan dalam soal ini,
A₁ peristiwa Adam terpilih sebagai ketua
A₂ peristiwa Dhanu terpilih sebagai ketua
A₃ peristiwa Shinta terpilih sebagai ketua
B adalah peristiwa naiknya iuran anggota
(B|Aᵢ), peristiwa naiknya iuran anggota jika terpilih calon ke-i dengan i = 1, 2, 3
Diketahui
P(A₁) = 0.3
P(A₂) = 0.4
P(A₃) = 0.2
P(B|A₁) = 0.4
P(B|A₂) = 0.6
P(B|A₃) = 0.5
Peluang terjadinya kenaikan iuran anggota P(B) merupakan peluang marginal sehingga dapat diperoleh dengan cara
P(B) = P(B|A₁). P(A₁) +P(B|A₂). P(A₂) + P(B|A₃) P(A₃)
= 0,4 0,3 + 0,6 0,4 + 0,5 0,2
= 0,12 + 0,24 + 0,10
= 0,46
*******
Lebih banyak pembahasan soal-soal Persiapan UTBK (Penalaran Matematika) dapat anda baca di


