Sebuah wadah air berbentuk kerucut sempurna dengan kedalaman 15 cm dan diameter 12 cm. Wadah tersebut berisi air dan diletakkan di halaman rumah. Pada siang hari yang terik air dari dalam wadah tersebut menguap sehingga ketinggian air berubah dengan kecepatan penguapan

Daftar Isi

Sebuah wadah air berbentuk kerucut

Sebuah wadah air berbentuk kerucut sempurna dengan kedalaman 15 cm dan diameter 12 cm. Wadah tersebut berisi air dan diletakkan di halaman rumah. Pada siang hari yang terik air dari dalam wadah tersebut menguap sehingga ketinggian air berubah dengan kecepatan penguapan 9/10π cm/jam. Laju perubahan volume pada saat ketinggian air 10 cm adalah ⋯ cm³/jam.

Pembahasan

Soal di atas merupakan aplikasi pada materi turunan fungsi lebih tepatnya merupakan soal dengan aturan rantai pada turunan fungsi aljabar.

Sahabat pintar matematika yang luar biasa, ijinkan saya menyampaikan pembahasan dengan penjelasan sederhana sebagai berikut.

Untuk menyelesaikan permasalahan tersebut pertama tama kita buat model / sketsa wadah air tersebut. Pada soal dikatakan wadah berbentuk kerucut terbalik dengan diameter 12 cm (ini berarti jari-jari wadah air setengah dari diameter yaitu 6 cm) dengan ketinggian wadah 15 cm, karena air penuh maka kita asumsikan tinggi air mula-mula atau h₁ sama dengan tinggi wadah yaitu 15 cm.

Setelah mengalami penguapan, ketinggian air menurun seiring berjalannya waktu. Pada soal dipermasalahkan laju perubahan volume saat ketinggian air 10 cm ini kemudian kita sebut sebagai h₂, dengan demikian karena perubahan ketinggian maka terjadi perubahan jari-jari permukaan air selanjutnya jari-jari setelah air menguap saya disebut r2.

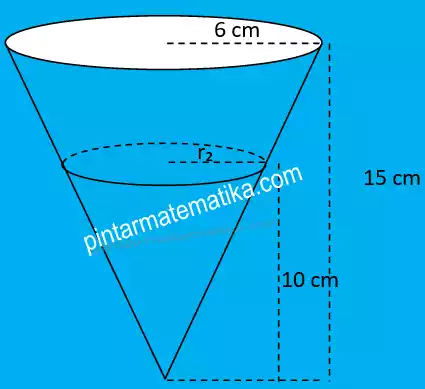
sketsa gambar : sebuah wadah air berbentuk kerucut

Dari sketsa dapat dituliskan
h₁ = 15 cm
r₁ = 6 cm
h₂ = 10 cm
sementara r₂ perlu dihitung.
maka dengan menggunakan perbandingan dapat diperoleh r₂ dengan cara sebagai berikut
h₁ . r₂ = h₂ . r₁
15 cm. r₂ = 10 cm . 6 cm
r₂ = 60 cm : 15 cm
r₂ = 4 cm

Pada soal disebutkan air dari dalam wadah tersebut menguap sehingga ketinggian air berubah dengan kecepatan penguapan $\frac{9}{10\pi}$ cm/jam
Perubahan ketinggian seiring berubahnya waktu dapat dituliskan sebagai $\frac{dh}{dt}$ sehingga diketahui

$\frac{dh}{dt} =\frac{9}{10\pi}$
Sedangkan yang menjadi pertanyaan utama adalah Laju perubahan volume seiring perubahan waktu atau

$\frac{dV}{dt}$
Laju perubahan volume sesuai perubahan waktu dapat diperoleh dengan menggunakan formula aturan rantai sebagai berikut

$\frac{dV}{dt}=\frac{dV}{dh}\times\frac{dh}{dt}$

Dari formula tersebut kita membutuhkan laju perubahan volume air berdasar perubahan ketinggan atau $\frac{dV}{dh}$
V = ⅓πr²h

$\begin{matrix}\frac{dV}{dh}=\frac{1}{3}\pi{(r_2)}^2\\\\\;=\frac{1}{3}\ pi{4}^2\\\\=\frac{16}{3}\pi\;\\\end{matriks}$

Langkah selanjutnya kita subtitusikan kedalam persamaan laju perubahan volume

$\begin{matrix}\frac{dV}{dt}=\frac{dV}{dh}\times\frac{dh}{dt}\\\\\;\;\frac{dV}{ dt}=\frac{16}{3}\pi\times\frac{9}{10\pi}\\\end{matriks}$

dengan menyederhanakan persamaan tersebut, kita peroleh laju perubahan volume pada saat ketinggian air dalam wadah 10 cm, yaitu

$\begin{matrix}\frac{dV}{dt}=\frac{8\ kali 3}{5}\\\\\;\;\;=\frac{24}{5}\\\\\;\;\;\;\;\;\;\;\;\;\ ;\;\;\;\;\;\;=4\frac{4}{5}\;cm^3/jam\\\end{matriks}$

dengan demikian, laju perubahan volume pada saat ketinggian air 10 cm adalah 4,8 cm³ per jam.

Jawaban E

*******

Lebih banyak pembahasan soal-soal Persiapan UTBK (Penalaran Matematika) dapat anda pelajari

kunjungi kak RH YT Channel : taklukan soal UTBK

Sebuah wadah air berbentuk kerucut

Sebarkan ini:

Posting terkait: