6 Perbandingan Trigonometri Contoh Soal : Sebuah kapal sedang berlabuh di dermaga dengan posisi menghadap ke menara

Daftar Isi

Perbandingan Trigonometri

Perbandingan trigonometri merupakan perbandingan sisi sisi pada segitiga siku siku, untuk mempermudah sisi sisi yang bersesuaian dapat diberi istilah seperti berikut ini.

Perhatikan gambar berikut dan penjelasannya!

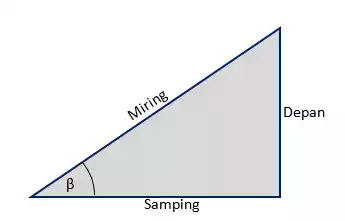
Penjelasan :

Sisi depan adalah sisi yang berada di depan sudut β selanjutnya kita persingkat dengan (de)
Sisi samping adalah sisi yang berada di samping sudut β selanjutnya kita persingkat dengan (sa)
Sisi miring adalah sisi yang berada di depan sudut siku siku selanjutnya kita persingkat dengan (mi)

Hubungan perbandingan sudut lancip dengan panjang sisi sisi suatu segitiga siku siku dinyatakan dengan definisi berikut

Sinus β

Sinus β merupakan penyebutan perbandingan sisi didepan sudut β dan sisi miring pada segitiga siku siku, sinus β dituliskan dengan

$sinus\;\beta=\frac{sisi\;didepan\;sudut\;\beta}{sisi\;miring}$

Cosinus β

Cosinus β merupakan penyebutan perbandingan sisi di samping sudut β dan sisi miring pada segitiga siku siku, cosinus β dituliskan dengan

$cosinus\;\beta=\frac{sisi\;disamping\;sudut\;\beta}{sisi\;miring}$

Tangen β

Tangen β merupakan penyebutan perbandingan sisi di depan sudut β dan sisi di samping sudut β pada segitiga siku siku, tangen β dituliskan dengan

$tangen\;\beta=\frac{sisi\;didepan\;sudut\;\beta}{sisi\;disamping\;sudut\;\beta}$

Cotangen β

Cotangen β merupakan kebalikan dari tangen β apabila keduanya dikalikan hasilnya sama dengan satu. Cotangen β dituliskan dengan rumus

$cotangen\;\beta=\frac{sisi\;disamping\;sudut\;\beta}{sisi\;didepan\;sudut\;\beta}$

Secan β

Secan β merupakan kebalikan dari Cosinus β, sepertihalnya cotangen dan tangen maka secan β apabila dikalikan dengan Cosinus β hasilnya sama dengan satu. Secan β dituliskan sebagai

$secan\;\beta=\frac{sisi\;miring}{sisi\;disamping\;sudut\;\beta}$

Cosecan β

Jangan salah inget ya, cosecan memang mirip pelafalannya dengan secan akan tetati cosecan β bukan kebalikan dari secan β. Cosecan β merupakan kebalikan dari sinus β yang keduanya jika dikalikan hasilnya juga sama dengan satu, dituliskan dengan

$cosecan\;\beta=\frac{sisi\;miring}{sisi\;didepan\;sudut\;\beta}$

Mari kita jadikan catatan

$\begin{matrix}Sin\beta=\frac{{\color{Red}de}pan}{{\color{Red}mi}ring}\;\;\;\\\\cos\beta=\frac{{\color{Red}sa}mping}{{\color{Red}mi}ring}\;\\\\tan\beta=\frac{{\color{Red}de}pan}{{\color{Red}sa}mping}\;\\\\cot\beta=\frac{{\color{Red}sa}mping}{{\color{Red}de}pan}\\\\sec\beta=\frac{{\color{Red}mi}ring}{{\color{Red}sa}mping}\\\\cosec\beta=\frac{{\color{Red}mi}ring}{{\color{Red}de}pan}\;\;\;\;\;\\\end{matrix}$

Contoh Soal dan Pembahasan

Nomor 1

Sebuah kapal sedang berlabuh di dermaga dengan posisi menghadap ke menara. Seorang pengamat yang berada di puncak menara melihat ujung depan kapal dengan sudut depresi 60 derajat dan ujung belakang dengan sudut depresi 30 derajat. jika tinggi pengamat 1,5 m, tinggi menara 40 m, dan dasar menara berada 20 m diatas permukaan laut, tentukan penjang kapal tersebut!

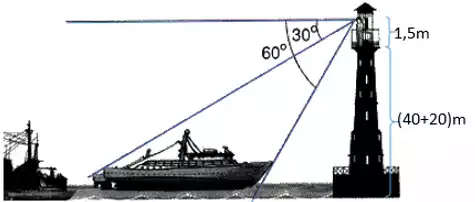
Pembahasan

Gambar pada soal dapat diilustrasikan menjadi sederhana, sebagai berikut

$PQ=PR-QR$

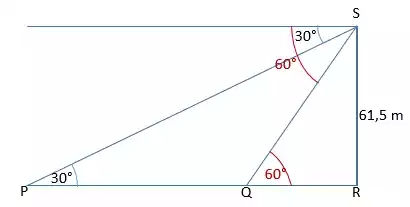
Untuk menyelesaikan soal ini, kita manfaatkan

$tan\beta=\frac{sisi\;depan}{sisi\;samping}$

Pada segitiga QRS berlaku

$\begin{matrix}tan60^\circ=\frac{SR}{QR}\;\;\;\;\;\;\;\\\\\sqrt{3}=\frac{61,5}{QR}\\\\QR=\frac{61,5}{\sqrt{3}}\\\end{matrix}$

Pada segitiga PRS berlaku

$\begin{matrix}tan30^\circ=\frac{SR}{PR}\;\;\;\;\\\\\frac{1}{3}\sqrt{3}=\frac{61,5}{PR}\\\\\;\;\;\;\;\;\;PR=3\times\frac{61,5}{\sqrt{3}}\\\end{matrix}$

jadi, panjang kapal tersebut adalah 41√3 meter atau ±71,01 meter

Nomor 2

Diketahui segitiga siku-siku ABC seperti pada gambar, jika panjang BC = 6 cm tentukan panjang AB dan AC

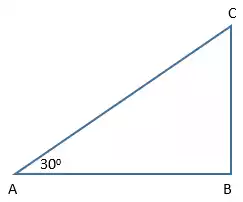
Pembahasan

Pertama tama mari kita ingat kembali tentang istilah

AB sebagai sisi “samping”
BC sebagai sisi “depan”
AC sebagai sisi “miring”

Jawaban dari soal diatas

Mencari AB

AB merupakan sisi samping, trigonometri yang bersesuaian adalah tangen, maka

b. Mencari AC

AC merupakan sisi miring, trigonometri yang bersesuaian adalah sinus dan cosinus

Misal kita pakai sinus, maka

Nomor 3

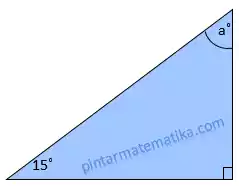
Dua orang siswa dengan tinggi 1½ m sedang melakukan penghormatan bendera siswa pertama dan kedua berjarak 12m, sudut elevasi siswa pertama-dan kedua masing-masing 60 dan 30 seperti pada gambar ilustrasi berikut:

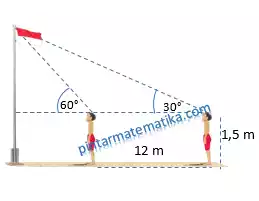
Tentukan tinggi tiang bendera!

Pembahasan

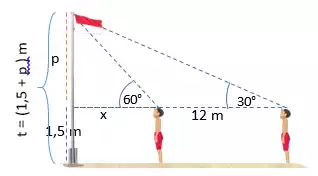
Persamaan 1

$\begin{matrix}tan60^\circ=\frac{p}{x}\;\;\;\;\;\;\;\;\;\;\;\;\;\\\\\;\;\;\;\;\;\;p=x.tan60^\circ\\\\p=x\sqrt{3}\\\end{matrix}$

Persamaan 2

$\begin{matrix}tan30^\circ=\frac{p}{x+12}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\\\;\;\;\;\;\;p=(x+12)tan30^\circ\\\\\;\;p=(x+12)\frac{1}{3}\sqrt{3}\\\end{matrix}$
Dari persamaan 1 dan persamaan 2

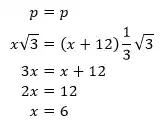
$\begin{matrix}p=x\sqrt{3}\\\\\;\;\;=6\sqrt{3}\\\end{matrix}$

Jadi

$\begin{matrix}t=(1,5+p)\;m\\\\\;\;\;\;\;\;\;=(1,5+6\sqrt{3})\;m\\\\\\\end{matrix}$

Nomor 4

Sebuah tangga yang panjangnya 8 meter bersandar pada tembok sebuah rumah. Kaki tangga membentuk sudut 3o˚ dengan tanah tentukan jarak ujung bawah tangga dengan rumah!

Pembahasan

$\begin{matrix}\;cos30=\frac{sa}{mi}\\\frac{1}{2}\sqrt{3}=\frac{j}{8}\\\;\;\;\;\;\;\;\;2j=8\sqrt{3}\\\;\;\;\;\;\;\;\;\;\;j=4\sqrt{3}\\\end{matrix}$

dengan demikian, jarak ujung tangga dengan tembok adalah $4\sqrt{3}$

Nomor 5

Seorang anak sedang berada di puncak sebuah gedung Ia melihat seekor sapi yang sedang makan rumput di sebelah gedung. Jika jarak sapi dengan gedung 120 m dan sudut depresi anak terhadap sapi 30°, tentukan tinggi gedung tersebut!

Pembahasan

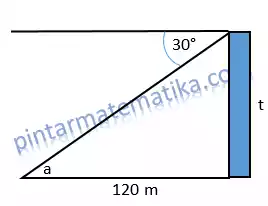
Berlaku nilai a = 30°

$\begin{matrix}tan30=\frac{de}{sa}\\\;\;\;\;\;\;\frac{\sqrt{3}}{3}=\frac{t}{120}\\\;\;\;\;\;\;\;\;\;\;\;\;\;3t=120\sqrt{3}\\\;\;\;\;\;\;\;\;\;\;\;\;\;t=40\sqrt{3}\\\end{matrix}$

Nomor 6

Diketahui tan15 = P tentukan nilai trigonometri berikut dalam P !

Sin15
Cos15
Tan75
Sin75

Pembahasan

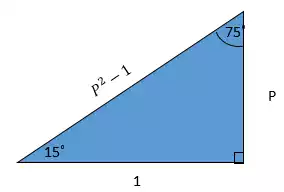
$\begin{matrix}a+15+90=180\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;a=180-90-15\\a=75\;\;\\\end{matrix}$
$tan15=p=\frac{p}{1}\Rightarrow\frac{de=p}{sa=1}$

Note: Sisi miring diperoleh dengan teorema phytagoras
Sehingga

Untuk sudut 15˚, depan = P, samping = 1, miring = p² – 1 , maka
$a.\;\;sin15=\frac{de}{mi}=\frac{p}{p^2-1}$
$b.\;\;cos15=\frac{sa}{mi}=\frac{1}{p^2-1}$

Untuk sudut 75˚ , depan = 1, samping = p, miring = p² – 1
$c.\;\;tan75=\frac{de}{sa}=\frac{1}{p}$
$d.\;\;sin75=\frac{de}{mi}=\frac{1}{p^2-1}$
Nomor 7

Seseorang yang berjarak 12 m melihat ke puncak sebuah pohon dengan sudut elevasi 60°. Jika tinggi pandangan orang tersebut 120 cm, berapa tinggi pohon tersebut !

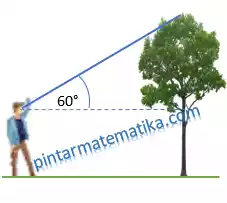
Pembahasan

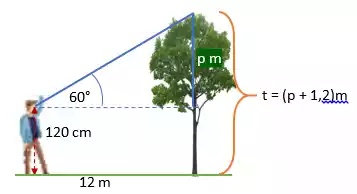
berlaku

$\begin{matrix}tan60^\circ=\frac{p}{12}\\\;\;\;\;\;\;\sqrt{3}=\frac{p}{12}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;p=12\sqrt{3}\\\end{matrix}$

Sehingga

$\begin{matrix}t=(p+1,2)m\\\;\;\;\;\;\;\;\;\;=(12\sqrt{3}+1,2)m\\\textrm{atau}\\\;\;\;\;\;\;\;\;\;=(1,2+12\sqrt{3})m\\\end{matrix}$

Berikut merupakan kumpulan soal-soal pilihan dari BAB Polinomial (Suku Banyak) dan Trigonometri yang dapat dijadikan referensi belajar untuk persiapan PSAS Mata pelajaran Matematika Kelas 11 Kurikulum Merdeka.

Soal Soal Mengenai Trigonometri

1 Soal dan Pembahasan Aturan Cosinus

2 Soal dan Pembahasan Aplikasi Perbandingan Trigonometri UTBK

∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗

Lebih banyak pembahasan soal-soal Persiapan UTBK (Penalaran Matematika) dapat anda baca di

kunjungi kak RH YT Channel : taklukan soal UTBK